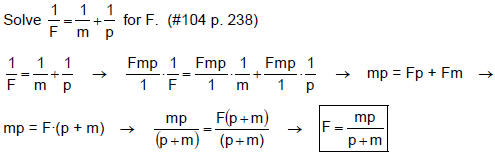|
|
Functions, Equations, and Inequalities
2.5 More Equation Solving
I. Rational Equations
Equations which contain rational expressions are called rational equations.
We will use a four
step process for solving rational equations.
Step 1:
Identify any restrictions on the domain by setting each denominator equal to
zero and
solving for x.
Step 2:
Multiply every term on both sides of the equation by the Least Common
Denominator
(LCD) to eliminate all of the denominators.
Step 3: Solve the resulting equation.
Step 4: Exclude any solutions which are restrictions on the domain.
Example 1
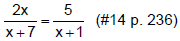
Restrictions on the Domain: x ≠ –7 and x ≠ –1 LCD: (x +
7)·(x + 1)
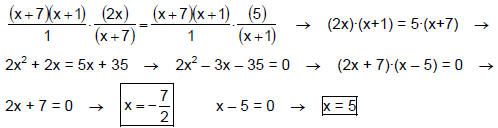
Since neither of these x-values is a restriction on the
domain, they are both valid
solutions.
Example 2
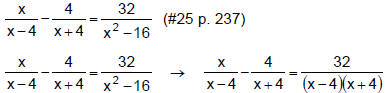
Restrictions on the Domain: x ≠ – 4 and x ≠ 4 LCD: (x +
4)·(x – 4)
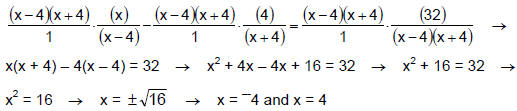
Since both of these x-values are restrictions on the
domain, this equation has
no solution.
II. Radical Equations
A radical equation is an equation in which at least one term has a
variable under a radical.
We will use a four step process for solving radical equations.
Step 1: Isolate the radical on one side of the equal sign.
Step 2: Raise both sides of the equation to the appropriate power to clear the
radical.
Step 3: If the resulting equation still contains a radical, repeat steps 1 and
2.
When the equation contains no radical, solve the equation for x.
Step 4:
Anytime you raise both sides of an equation to an even power, you must check
your
solutions in the original equation.
Example 3
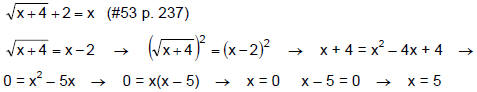
checking 0:
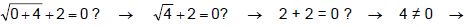
0 is not a valid solution.
checking 5:
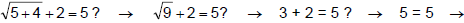
5 is a valid solution.
Example 4
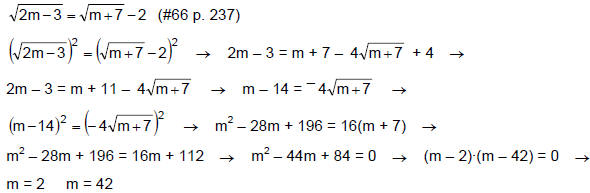
checking 2:
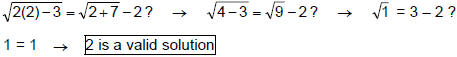
checking 42:
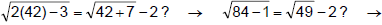
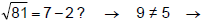 is not a valid
solution. is not a valid
solution.
III. Solving an Equation for a Specified Variable
When we solve an equation for a specified variable, we must undo the operations
which have
been done on the specified variable by doing the opposite operations in the
opposite order.
We work from the outside in. First we undo Addition / Subtraction, then
Multiplication / Division,
then Exponents, and finally Parentheses.
Example 5
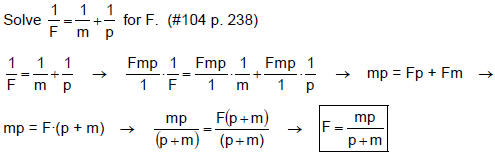
|


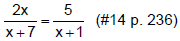
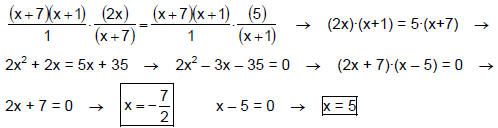
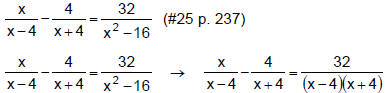
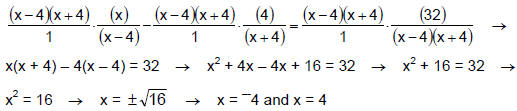
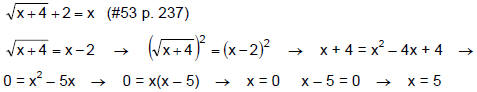
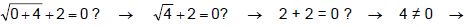
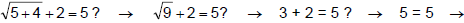
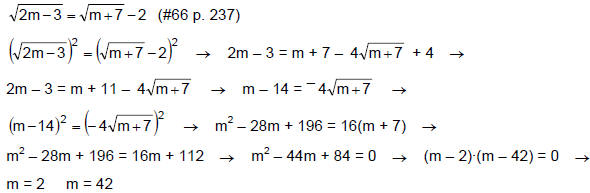
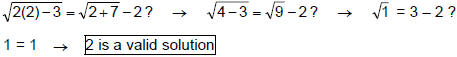
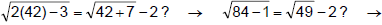
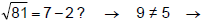 is not a valid
solution.
is not a valid
solution.