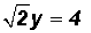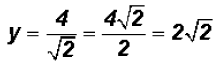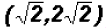|
Home |
SOLVING SYSTEMS OF EQUATIONSMany applied problems are modeled by two or more
equations. When this happens, we talk about a All systems of equations could be solved graphically, but
this method tends to give us inaccurate The Substitution Method works extremely well for finding
solutions of Systems of Linear and Nonlinear Strategy for Solving Systems of Equations by the Substitution MethodStep 1: Solve any one of the equations for one
variable in terms of the other. If one of Step 2: Substitute the expression found in Step 1
into the other equation. You should Please note that ONLY at the point of intersection two
equations are equal to Step 3: To find the value of the second variable,
back-substitute the value of the variable Step 4: Form an ordered pair with the values found
in Step 3 and Step 4. This is the Strategy for Solving Systems of Equations by the Addition MethodStep 1: If necessary, rewrite both equations in the
same form so that the variables and Step 2: If necessary, multiply either equation or
both equations by appropriate numbers Step 3: Write the equations one below the other,
draw a horizontal line, then add each of Step 4: To find the value of the second variable,
back-substitute the value of the variable Step 5: Form an ordered pair with the values found
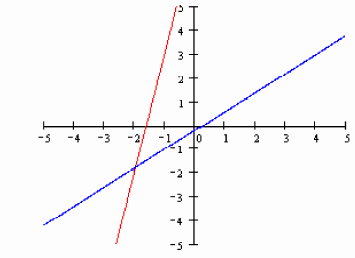
in Step 4 and Step 5. This is the Example 1: -5x = y = 8 -4x + 5y = -1 Below is a pictorial representation of the system. The
point of intersection is considered the solution
Solving any System of Equations graphically often does not
give use the correct solution. Actually, the solution is Substitution MethodStep 1: y = 5x + 8 Step 2: -4x + 5(5x + 8) = -1 Step 3:
Step 4: Addition MethodStep 1: Step 2: -5(-5x + y) = -5(8) Step 3:
The x-coordinate of the point of intersection Step 4:
Step 5:
Example 2:
We will use the Substitution Method, which means that we
have to solve one of the equations for Step 1: Using
Step 2:
Therefore, the x-coordinates for the solutions are
Step 3: Using the quadratic equation
Using the circle
It can be concluded, that this will happen for every
x-value, and further Example 3:
We will use the Substitution Method again, but this time,
we will solve the second equations for x2.
Next, let's back-substitute into the equation
Thus, the y-coordinates for the solutions are 1 and
-2.
You can now find the corresponding xcoordinates. Example 4:
Let's use the Substitution Method and solve the first equation for x.
Using the Square Root Property we find
which means that y = 2 and y = -2. Since NOT both equations are linear, we must find the values for y using both original equations.Using the linear equation x + y = 0: •If y = 0,then x + 0 = 0 •If y = 2,then x + 2 = 0 •If y = -2,then x - 2 = 0 Using the polynomial equation
Thus, one solution is t can be concluded, that this will happen for every x-value, and further
investigation Example 5:
We will use the Substitution Method, which means, that we
have to solve one of the equations for Next, we will back-substitute into the equation
This is a quadratic equation that is not factorable. Therefore, we have to use the Quadratic Formula.
The x-coordinates for the points of intersection are imaginary numbers. Therefore, there are no solutions to this system. The two graphs do not intersect. Example 6:
In this case, both equations are already solved for y.
Therefore, we will definitely use the
Since not both equations are linear, we must find the
values for y using both original equations. •If x = 2,then y = 2 - 2 = 0 •If x = 1,then y = 1 - 2 = -1 Using the quadratic equation •If x = 2, then Thus, just like in the case of the linear equation, the
quadratic equation produces It can be concluded, that this will happen for every x-value, and further
investigation Example 7:
Let's use the Substitution Method since the first equation
is already solved for y. Therefore, we can
Using the Square Root Property we find
which means that
Since NOT both equations are linear, we must find the values for y using both original equations. Using the linear equation y = 2x: •If •If Using the rational equation xy = 4: •If Thus, just like in the case of the linear equation, the
rational equation produces It can be concluded, that this will happen for every
x-value, and further investigation |


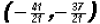 as
you will see below.
as
you will see below.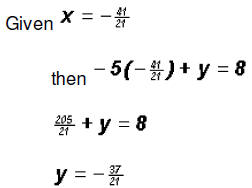
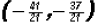
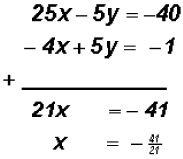
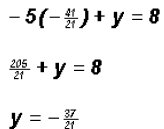
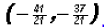
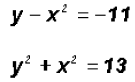
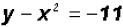 we
find
we
find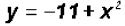
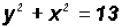 to
get
to
get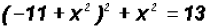
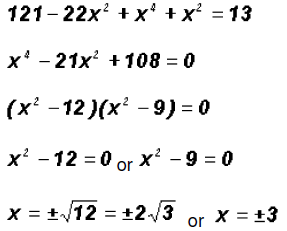
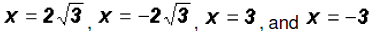
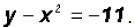
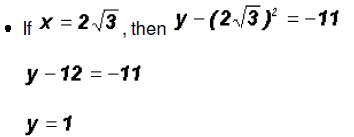
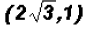
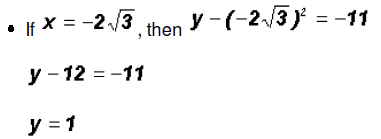
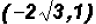 is
another solution
is
another solution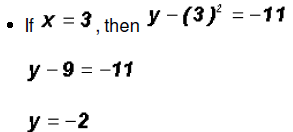
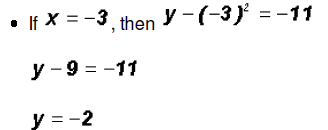
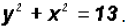
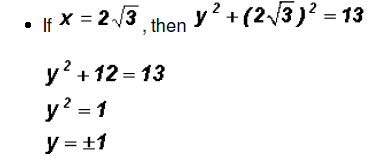
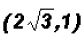 but
there is another solution, namely,
but
there is another solution, namely,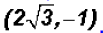 This
solution did not show up when we used the quadratic
This
solution did not show up when we used the quadratic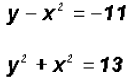
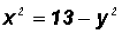
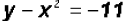
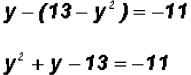
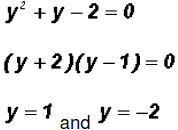
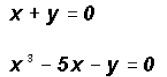
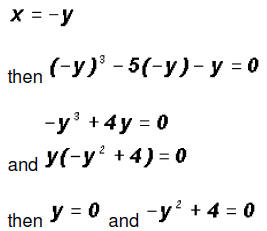
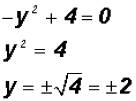

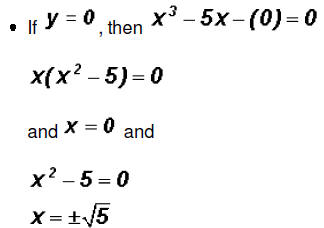
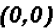 but
there are two other solutions, namely
but
there are two other solutions, namely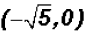
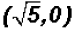 These
solutions did not show up when we used the linear equation,
These
solutions did not show up when we used the linear equation,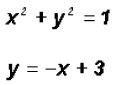
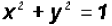
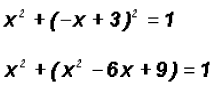
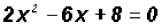
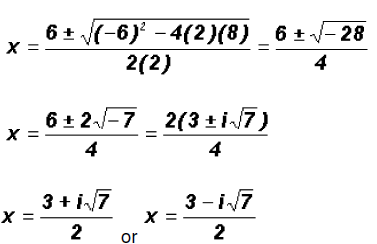
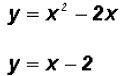
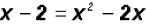 Notice, that we are simply setting the two
equations equal to each other
Notice, that we are simply setting the two
equations equal to each other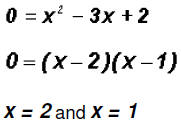
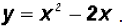
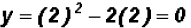
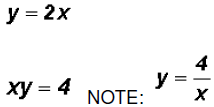
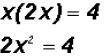
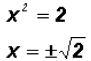
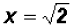 and
and
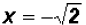
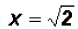 ,then
,then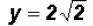
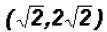
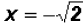 ,then
,then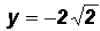
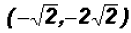
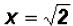 ,then
,then