Solving Equations by Clearing Fractions
• Recall how to solve an equation
containing fractions. We found the LCD
of all denominators and “cleared
fractions” by multiplying both sides of
the equation by the LCD.
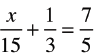 |
Solve for x and Check
Solution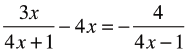
|
Your Turn: Solve for x and
Check Solution
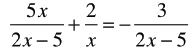 |
Solve for x and Check
Solution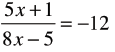
|
| Solve for x Graphically
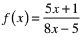 find all x such
that f(x)=-12 find all x such
that f(x)=-12
a. Sketch the graph of f on graph paper. Label the
zeros of f with their
coordinates and the asymptotes of f with their equations.
b. Add the graph of y = -12 to your plot and estimate the coordinates of
where the graph of f intersects the graph of y = -12.
c. Use the intersect utility on your calculator to find better
approximations of the points where the graphs of f and y = -12
intersect.
d. Solve the equation f(x) = 2 algebraically and compare your solutions
to those found in part (c). |
Your Turn
• Page 677: 1 and 2 |
Chapter 8
Section 1
Introduction to Radicals |
Start by Solving: x2 = a
• Three cases:
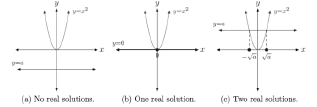 |
| Define 5. The solution of x2=a
are called "square root of a" • In the
case a<0 ,the equation x2=a has no real solutions.
• In the case a=0 ,the equation x2=a
has one real solution ,namely x=0
• In the case a>0, the equation x2=a
has two real solution ,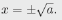 The The
notation 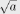 calls for the positive
square root of a ,that is ,the positive solution of x2=a.
The notation calls for the positive
square root of a ,that is ,the positive solution of x2=a.
The notation 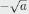 calls for the negative
square root of a , that is , calls for the negative
square root of a , that is ,
the negative equation solution of x2=a. |
Examples
• Solve the following graphically and
algebraically:
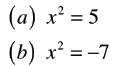 |
Higher Order Roots
• Start by Solving: x3 = a
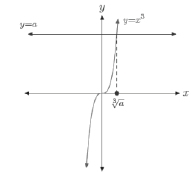 Figure
2.The graph of y=x3 inter-
sect the graph of y=a in exactly one
place. |
Square Roots
• The number c is a square root of a if
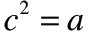
Example: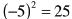
So, -5 is a square root of 25 |
Principal Square Root
• The principal square root is a nonnegative
number given by:
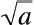
• The negative square root is given by:
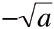 |
Note!
• For all real values of a
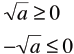 |
Simplify The Square Root
of a Square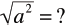
|
| • For any real number a
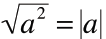
The principal square root of a2 is the
absolute value of a |
| Simplify
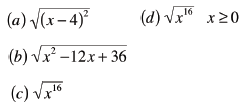 |
Higher Ordered Roots
• The value c the nth root of a if
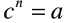
• The nth root of a number is denoted
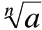
|
Examples, Use Graph or
Table to Check
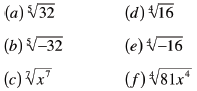 |
The nth root of an
• To simplify 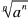 where a is any real where a is any real
• The value of 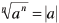 when n is even when n is even
• The value of 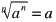 when n is odd when n is odd |
Definition of a Rational
Exponent
• The nth root of of a is the same as
raising a to the power of 1/n
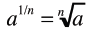 |
• Also, given 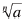 exists then exists then
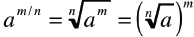 |
Examples: Rewrite in radical
notation or in rational
exponents
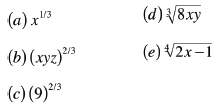 |
| Simplify
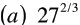
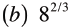
|
Examples
• Use the table (where possible) to
determine if the following simplifications
are correct
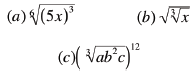 |
| Negative Exponents
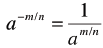 also also
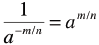
|