|
Home |
Linear Equations in Linear AlgebraA system of linear equations is two or more linear equations considered at the same time. A solution to a system of linear equations (in two variables) is an ordered
pair of real numbers x + 2y = 8 is a linear equation in two variables. 2x - y = 6 is also a linear equation in two variables.
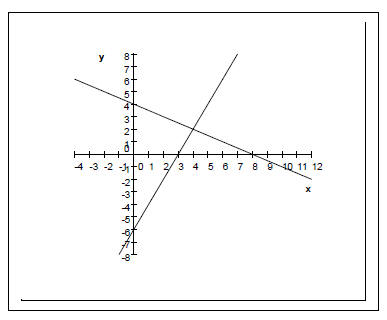
It has only one solution. What is it? Why is (2,3) not a solution to the system
Why is (5,4) not a solution to the system
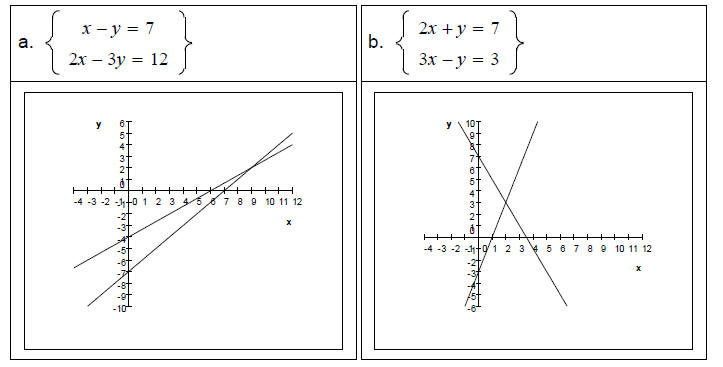
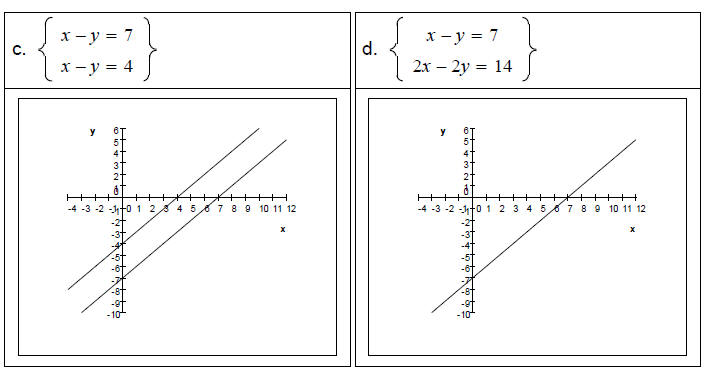
Solving Systems of Linear Equations by the Graphical Method Example 1 Solve each system of linear equations by inspecting the graphs below it.
Solving Systems of Linear Equations by Substitution How to use the substitution method to solve systems of linear equations: Example 2 Solve the system
Step 1 Solve the equation x - 2y = 3 for x. Step 2 Substitute the expression 2y + 3 for x in the equation 3x - 8y = 7. Step 3 Solve the equation 3(2y + 3) - 8y = 7 for y. Step 4 Since y = 1, substitute 1 for y in the equation x = 2y + 3 found in Step 1 and find x. Step 5 Since the equation x - 2y = 3 is equivalent to the equation x = 2y + 3
just used in Example3 Solve the system
Step1 Solve the equation 2x-y=12 for y. Step2 Since y=2x-12,substitute the expression 2x-12 for y in the equation 6x-3y=10. Step3 Solve the equation 6x-3(2x-12)=10 for x. Step4 Is the equation you found in Step3 a true statement or a false statement? Step5 What is the solution set? Example 4 Solve the system
The next method we will study is called the addition or
elimination method. Let’s see how this method works by using it to solve the
system What we want to do is add the two equations together in
such a way that either the
The y-variable goes away because its coefficients in the two equations are additive opposites. That makes the y-terms add together to make 0y. Once we know the value of x, we can substitute it into either equation to find the value of y.
The only solution is (3,1) which we should check in the
other equation 3x + 5y = 14 Example 5 Solve the system
Example 6 Solve the system
Example 7 Solve each system using the elimination method.
|


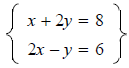 is
a system of linear equations in two variables.
is
a system of linear equations in two variables.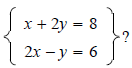
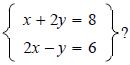
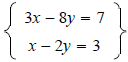 using
the substitution method.
using
the substitution method.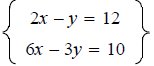 using the substitution method.
using the substitution method.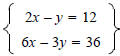 using the substitution method.
using the substitution method.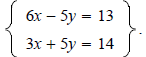
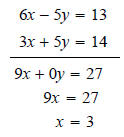
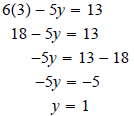
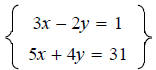 using the elimination method.
using the elimination method.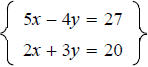 using the elimination method.
using the elimination method.