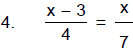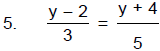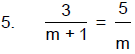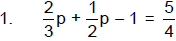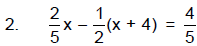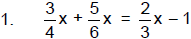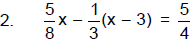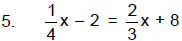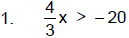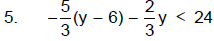Solving Multiple-Step Equations
Solving Multiple-Step Equations (Part 1) – Variable on
One Side
Instructions:
Follow along with video and fill in the blanks as indicated. Space has been
provided for
you to show all work on this sheet and take any additional notes.
Example: Copy steps/answers from video.
1. 4x + 2x – 3 = 9
Fill in the blank(s):
| Equations that contain like terms must be
simplified ___________they can |
Examples: Copy steps/answers from video.
2. 7m – m + 5 = 14
3. 12y + 3y – 8y = –12 + 33
4. 4(a + 3) + 6a = –4
5. 14 – (6x + 2) + 8x = –14 + 20
Notes:
__________________________________________________________________________
________________________________________________________________________________
Problem Set: Solving Multiple-Step Equations – Part 1
Solve and check your solutions.
1. 4m – 6m + 8m = –20 – 4
2. –3x – 4 – 8x + 6 = –20
3. –6 + 8 = 4y + 3(y + 5) – 6
4. –6 + 8 = 4y – 3(y + 5) – 6
5. 2(m – 3) – 4(m + 6) = 18
Lesson 8 (cont’d): Solving Multiple-Step Equations
(Part 2) – Variable on Both Sides
Examples: Copy steps/answers from video.
1. 3x – 2 = 6x + 7
2. 4(x – 3) + 8 = 2x – 2 + 12
Fill in the blank(s):
Steps for Solving Linear Equations
1. Remove any _______________________and combine like
terms on each side of the equation.
2. Use the Addition Property of Equality to get:
a. the __________________ terms on ____________
and/or
b. the __________________ terms on the other side.
3. Use the Multiplication/Division Property of Equality to get
the __________________ of the variable term equal to a “1”.
4. ____________your answer. |
Copy steps/answers from video.
3. 3(a + 12) = 1 – 2(a – 5)
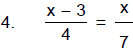
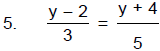
Problem Set: Solving Multiple-Step Equations – Part 2
Solve and check your solutions.
1. –5m + 3 = 2m – 4
2. –4x – 2(x + 5) – 3x = 13 + 8 + x
3. 3y + 2(y – 4) = 12 y + 5
4. 8m – (m + 2) + 4 = 4m – 7
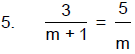
Lesson 8 (cont’d): Strategies – Decimals and Fractions
Examples: Copy steps/answers from video.
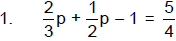
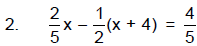
3. 0.3 – 0.5(x + 3) = 1.4 – 0.6x
4. 0.4(2x + 5) = 2.3 – (x + 3)
Notes:
_________________________________________________________________________
Problem Set: Solving Equations with Decimals and
Fractions
Solve by first clearing the fractions and decimals. Check at least two
solutions.
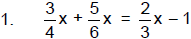
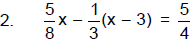
3. 2.1x + 6.5 = 4.1 – 3.9x
Solve without clearing the fractions or decimals.
4. 0.6 – 2(a – 1) = 0.2 + 5 – a
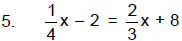
Lesson 8 (cont’d): Solving Inequalities
Fill in the blank(s):
An __________________ is two expressions
separated by one of
the following symbols:
Less than, <
Less than or equal, <
Greater than, >
Greater than or equal, > |
Examples: Copy steps/answers from video.
Fill in the blank(s):
Addition Property for Inequalities
Given an inequality, we can ______ the same number to
_______ sides of the inequality. |
Copy steps/answers from video.
3. y + 6 < 12
4. x – 3 > 12
5. 12 < – 4 + x
Consider the following inequality: Copy steps/answers from video.
2 < 3
2 < 3
Fill in the blank(s):
Multiplication/Division Property for
Inequalities
Given an inequality, you can multiply or divide ________sides by
the same non-zero number.
Note: _______________ the inequality symbol
when multiplying or dividing by a _______________number. |
Copy steps/answers from video.
7. –2x + 4 < 8
8. 2x + 4 < 8
Fill in the blank(s):
Steps for Solving Inequalities
1. __________________ each side by removing parentheses
and combining like terms, as needed.
2. Use the Addition Rule, if needed, to _____________ the
_____________ term on one side.
3. Use the Multiplication/Division Rule to make the
________________ a ____________.
Note: ___________________the inequality symbol when
multiplying or dividing by a _______________ number. |
Copy steps/answers from video.
9. 6x – 8x + 12 < 3x – 12
10. 3(x – 2) – 8x + 9 > –16 + 5
Problem Set: Solving Inequalities
Solve and check your solutions. Draw a number line graph of your solution.
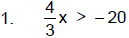
2. –8p + 5 > 21
3. 3m – 8m + 7 < 18 – 5
4. –2(x + 4) + 3x < 2x – 5
|
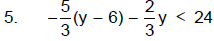
