Equations
The first thing we want to do is review basic solving of
equations. We will start with linear
equations.
A few key ideas to remember is when solving equations we are usually trying to
get the equation
to look like variable = number. We do this by adding, subtracting,
multiplying or dividing
quantities on both sides of the equation. Also, we should remember that removing
parenthesis
and combining like terms are always good ideas to do first.
Example 1:
Solve.
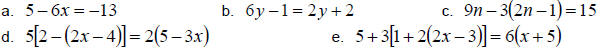
Solution:
a. We start by isolating the variable term by subtracting 5 from both sides,
then we divide by
–6 to get the variable = number.
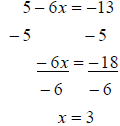
We generally write solutions to equations in a solution
set. So the solution is 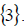
b. This time we will need to move all the terms containing variables to the same
side first.
Then we can simply solve as we did in part a.
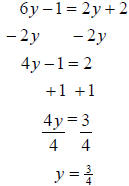
So the solution set is 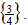
c. This time we start by distributing the –3 to remove the
parenthesis. Then we combine
like terms and continue as usual.
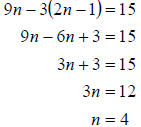 |
|
| |
| Subtract 3 from both sides |
| Divide by 3 on both sides |
| |
So the solution set is 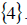
d. This example is a little more complicated. We need to use the distributive
property
several times to remove all the parenthesis. Then we can continue as we did
before.
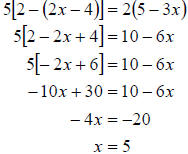 |
|
| Combining like terms |
| |
| |
| Add 6x and subtract 30 from both sides |
| Divide by -4 on both sides |
So the solution set is 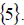
e. Again we carefully simplify each side and then solve for the variable. We get
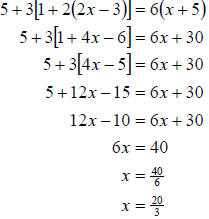 |
|
| |
| Combining like terms |
| Combining like terms again |
| Subtract 6x and add 10 from both sides |
| Divide by 6 on both sides |
| |
| |
So the solution set is 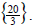
Another thing we want to remember is that when dealing with an equation that
contains fractions,
we usually want to start by clearing the fractions. We do this by multiplying
both sides of the
equation by the LCD (least common denominator).
Example 2:
Solve

Solution:
a. Since the LCD is clearly 4, we multiply both sides by 4 and continue solving
as in the last
example. We get
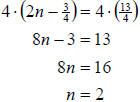
So the solution set is 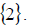
b. This time the LCD is 6. We must be very careful when
multiplying both sides by the LCD
this time. The key is to multiply each term by the LCD and then carefully
reduce. We
proceed as follows
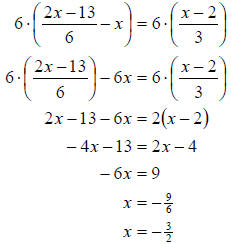
So the solution set is 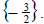
Lastly, we want to solve applications by using linear equations.
Example 3:
Your mechanic charges you $278 for performing a 30,000-mile checkup on you car:
This charge
includes $152 for parts and $42 per hour for labor. Set up an equation and use
it to find the
number of hours the mechanic worked on your car.
Solution:
First we need to assign a variable to the quantity we are looking for. Lets let
number of
hours worked. Now we can construct an equation. Since it is $152 for parts and
$42 per hour
labor we get the total cost is 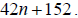 . Since the
charge for the checkup is $278 we get the . Since the
charge for the checkup is $278 we get the
equation 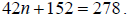 . Now we simply solve for n. . Now we simply solve for n.
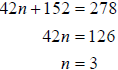
So the mechanic worked 3 hours on our car.
There are other, more complicated word problems. However, we will reserve
solving those in the
text when we review systems of equations, since it is easier to solve the more
complex type by
using a system of equations.
R.1 Exercises
Solve.
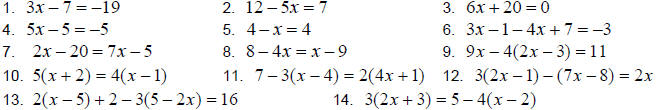
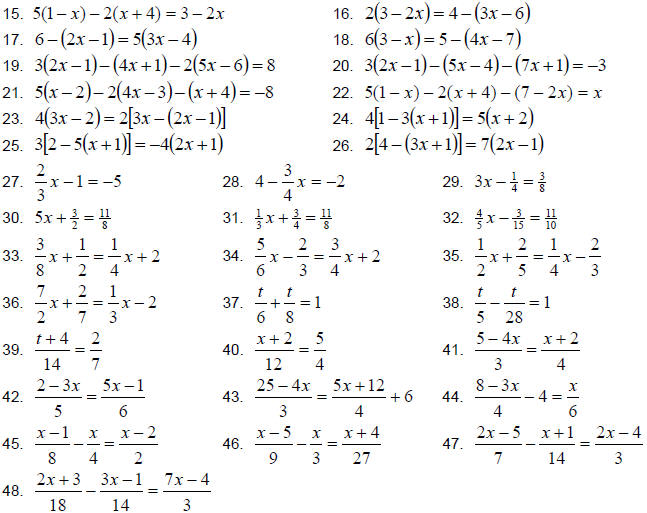
49. 6 times a number is increased by 10. The result is 94.
Find the number.
50. 4 less than three times a number is 32. Find the number.
51. 10 less than twice a number is 100. Find the number.
52. 3 times a number is increased by 1. The result is 19. Find the number.
53. A union charges monthly dues of $3 plus $.18 for each hour worked during the
month. A
union member’s dues for July were $31.80. Use an equation to find how many hours
were
worked in July.
54. The monthly income for a manager of an apartment complex was $3500. This
includes the
manager’s base salary of $2500 plus a 2.5% bonus on total sales. Set up an
equation and
use it to find the managers total sales for the month.
55. A technical hotline charges a customer $8 plus $.40 per minute to answer
questions about
software. Use an equation to find out how many minutes a customer was on with
the hotline
if they were charged $22.
56. Budget plumbers charged $465 for replacing a water heater and replacing
pipes to the water
heater. The charge included $365 for materials and $40 per hour for labor. Use
an equation
to find how many hours of labor were charged.
57. The monthly income for a manager of a mobile home
dealership was $3500. This includes
the managers base salary of $2500 plus a 1% commission on total sales. Use an
equation to
find the sales for the month.
58. Your mechanic charges you $278 for performing a 30,000-mile checkup on you
car: This
charge includes $152 for parts and $42 per hour for labor. Set up an equation
and use it to
find the number of hours the mechanic worked on your car.
Use the formula 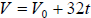 to answer the following
questions, where V is the final velocity, to answer the following
questions, where V is the final velocity,
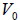 is the initial velocity, of a falling object,
and t is the time for the object to fall. is the initial velocity, of a falling object,
and t is the time for the object to fall.
59. Find the time required for a falling object to increase in velocity from 16
ft/sec to 128 ft/sec.
60. Find the time required for a falling object to increase in velocity from 2
ft/sec to 58 ft/sec.
Use the formula 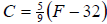 , where C is the Celsius
temperature and F is the Fahrenheit , where C is the Celsius
temperature and F is the Fahrenheit
temperature, to answer the following questions.
61. Find the Fahrenheit temperature when the Celsius temperature is −40°.
62. Find the Fahrenheit temperature when the Celsius temperature is 0°.
63. The length of a rectangle is 5 ft more than the width. If the perimeter is
30 ft, what are the
dimensions of the rectangle?
64. The width of a rectangle is 8 m less than the length. If the perimeter is 24
m, what are the
dimensions of the rectangle?
65. The length of a rectangle is three less than two times the width. If the
perimeter is 18 feet,
what are the dimensions of the rectangle?
66. The length of a rectangle is twice the width. If the perimeter is 300 feet,
what are the
dimensions of the rectangle?
67. The height of a triangle is 3 cm. If the area is 30 cm2, what is the length
of the base of the
triangle?
68. The base of a triangle is 15 cm. If the area is 75 cm2, what is the length
of the base of the
triangle?
69. One side of a triangle is 3 times the length of the first. The other side is
8 m less than twice
the first. If the perimeter is 22 m, what are the lengths of the sides of the
triangle?
70. One side of a triangle is 2 times the length of the first. The other side is
6 m less than the
first. If the perimeter is 26 m, what are the lengths of the sides of the
triangle?
|


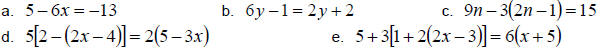
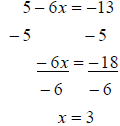
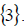
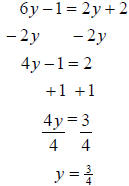
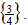
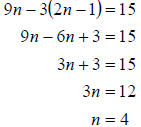
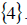
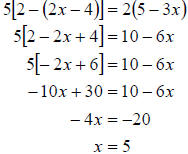
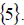
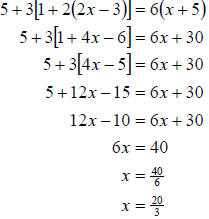
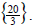

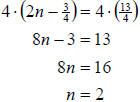
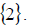
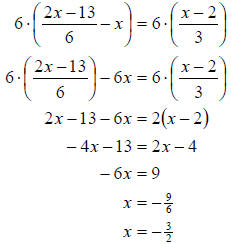
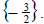
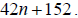 . Since the
charge for the checkup is $278 we get the
. Since the
charge for the checkup is $278 we get the 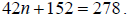 . Now we simply solve for n.
. Now we simply solve for n.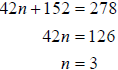
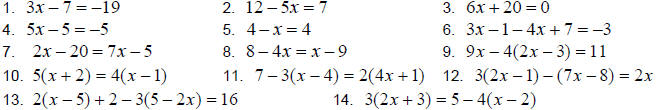
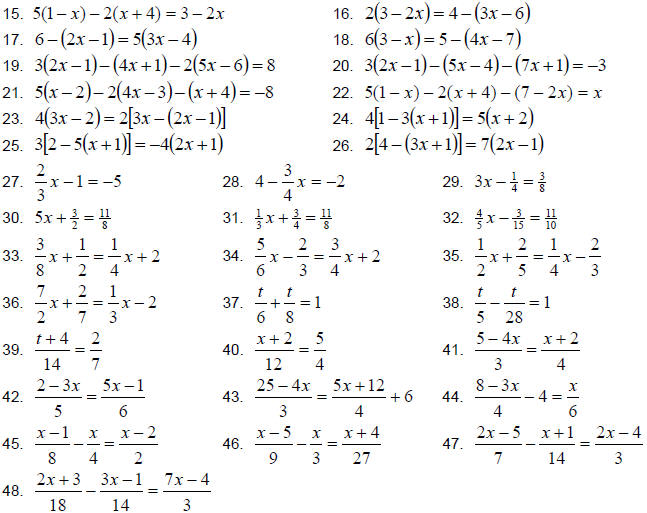
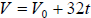 to answer the following
questions, where V is the final velocity,
to answer the following
questions, where V is the final velocity, 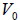 is the initial velocity, of a falling object,
and t is the time for the object to fall.
is the initial velocity, of a falling object,
and t is the time for the object to fall. 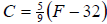 , where C is the Celsius
temperature and F is the Fahrenheit
, where C is the Celsius
temperature and F is the Fahrenheit