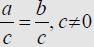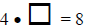|
|
Simplifying Expressions & Solving Equations
Simplifying Algebraic Expressions (3.1)
1) In algebra, a variable is an unknown quantity that
changes [or varies] in value
from one situation to another. A single letter usually represents the variable
2) The addends of an algebraic expression are called the terms.
3) A term that is only a number is called a constant term, or simply a constant.
A
term that contains a variable is called a variable term.
4) The number factor of a variable term is called the numerical coefficient. A
numerical coefficient of 1 is usually not written.
What are the numerical coefficients of the terms below?

5) Terms that are exactly the same, except that they may
have different
numerical coefficients are called like terms.
|
Like Terms |
 |
Unlike Terms |
 |
6) A sum or difference of like terms can be simplified
using the Distributive
Property.
Distributive Property
If a, b, and c are numbers, then ac +bc= (a+b)c =c( a+b)
Also, ac -bc= (a-b)c =c( a-b) |
• The Distributive Property guarantees that no matter what
number x is,
7x+2x=(7+2)x=9x [for example]
This is an example of combining like terms.
• An algebraic expression is simplified when all like terms have been combined.
• We can use the distributive property to combine like terms or to multiply
expressions.
• This property says that multiplication distributes over addition and
subtraction.
Simplify the expressions
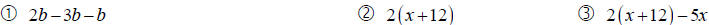
Solving Equations (Section 2.6)
1)An equation is mathematical statement that says that two expressions are
equal.
expression = expression
2) The solution to an equation is a number that when substituted for the unknown
quantity [variable] in the equation will result in a true statement when all the
arithmetic has been performed.
3) An equation is solved when the unknown quantity [variable] is determined.
4) To solve an equation, we will use properties of equality to write simpler
equations, all equivalent to the original equation, until the final equation has
the
form
x = number or number = x
Examples:
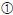 Is - 6 a
solution of-3k =12- k ? Is - 6 a
solution of-3k =12- k ?
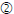 Is 1 a solution of 2(b
-3) =10 ? Is 1 a solution of 2(b
-3) =10 ?
Properties of equality for solving equations state that in
performing the same
operation on both sides of the equal sign in a true equation, the resulting
equation is still true.
Addition Property of Equality (2.6)
Let a, b, and c represent numbers.
If a = b, then a + c = b + c
In other words, the same number may be added to both sides of an
equation without changing the solution of the equation. |
Solve for x:
x - 4 = 3
To solve the equation for x, we need to rewrite the equation in the form
x = number.
To do so, we add 4 to both sides of the equation.
|
x - 4 = 3 |
|
|
x - 4 + 4 = 3 + 4 |
Add 4 to both sides. |
|
x = 7 |
Simplify. |
Check:
|
x - 4 = 3 |
original equation |
|
7 - 4 = 3 |
Replace x with 7. |
|
3 = 3 |
Simplify. True. |
Since 3 = 3 is a true statement, 7 is the solution of the
equation.
 Remember that we can get the variable
alone on either side of the Remember that we can get the variable
alone on either side of the
equation. x = 3 or 3 = x
Solve. Check each solution.
Write an equation that can be solved using the addition
property of equality.
Write an equation that can be solved using the multiplication property of
equality.
Multiplication Property of Equality (2.6)
Let a, b, and c represent numbers and let c ≠ 0.
If a = b, thena · c = b · c and = ,
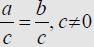
In other words, both sides of an equation may be
multiplied or divided
by the same nonzero number without changing the solution of the
equation. |
Solve for x:
-4x = 8
To solve the equation for x, we need to rewrite the equation in the form
x = number. To do so, we divide both sides of the equation by -4 and
then simplify.
To check, replace the x in the original equation with the solution.
|
4x = 8 |
original equation |
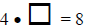 |
Replace x with 2. |
|
8 = 8 |
Simplify. True statement. |
Since 8 = 8 is a true statement, 2 is the solution of the
equation.
SIMPLIFY vs. SOLVE
• We simplify expressions and solve equations.
• To simplify an expression we write it in a less complicated form.
• To solve an equation means to find the number(s) that make the
equation true when substituted for its variable.
• Quite often we must simplify expressions on the left- or right-hand
sides of an equation when solving it.
Steps for Solving Linear Equations in One
• Step 1. If parentheses are present, use the distributive property to
remove parentheses.
• Step 2. Combine any like terms on each side of the equation.
• Step 3. Use the addition property to rewrite the equation so that
the variable terms are on one side of the equation and constant
terms are on the other side.
• Step 4. Use the multiplication property of equality to divide both
sides by the numerical coefficient of x to solve.
• Step 5. Check the solution in the original equation.
Translating Word Phrases into Expressions
the product of 5 and a number: 5x
twice a number: 2x
a number decreased by 3: x - 3
a number increased by 2: x + 2
four times a number: 4x
the sum of a number and 7: x + 7
three times the sum of a number and 7: 3(x + 7)
three times a number plus seven:
the quotient of 5 and a number:
four times the difference of a number and 5:
the difference of four times a number and 5:
the quotient of negative two and 4 times a number:
Linear Equations in One Variable and Problem Solving
(3.4)
Keyworrds and phrrases suggesttiing
addiittiion,, subttrracttiion,, mullttiiplliicattiion,,
division orr equuaallss..
| Addition |
Subtraction |
Multiplication |
Division |
Equal Sign |
| sum |
difference |
product |
quotient |
equals |
| plus |
minus |
times |
into |
gives |
| added to |
less than |
of |
per |
is / was |
| more than |
less |
twice |
divide |
yields |
| total |
decreased
by |
multiply |
divided
by |
amounts to |
increased
by |
subtracted
from |
double |
|
is equal to |
Problem-Solving Steps
1. Understand the problem. During this step, become comfortable with the
problem. Some ways of doing this are:
• Read and reread the problem.
• Choose a variable to represent the unknown.
• Construct a drawing.
• Propose a solution and check it. Pay careful attention to how you check your
proposed solution. This will help when writing an equation to model the
problem.
2. Translate the problem into an equation.
3. Solve the equation.
4. Interpret the results. Check the proposed solution in the stated problem and
state your conclusion.
1. Four times the difference of 12 and a number equals 72.
Find the number.
2. The difference of a number and 9 is 37 less the number. Find the number.
3. Four times the sum of a number and 2 is 24 less than the number times 8. Find
the number.
4. The product of 10 and a number is the same as 36 less twice that same number.
Find the number.
5. In a recent year, the two top-selling PC games were World of Warcraft and
The Sims 2: University Expansion Pack. The average price of World of
Warcraft is $14 more than the average price of Sims. If the total of these two
prices is $80, find the price of each game.
6. An Xbox 360 game system and several games are sold for $560. The cost of
the Xbox 360 is 3 times as much as the cost of the games. Find the cost of the
Xbox 360 and the cost of the games.
|



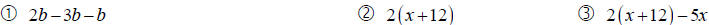
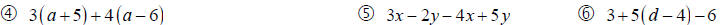
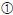 Is - 6 a
solution of-3k =12- k ?
Is - 6 a
solution of-3k =12- k ? 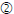 Is 1 a solution of 2(b
-3) =10 ?
Is 1 a solution of 2(b
-3) =10 ? Remember that we can get the variable
alone on either side of the
Remember that we can get the variable
alone on either side of the