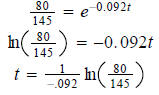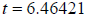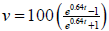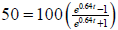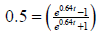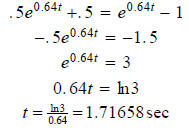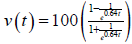|
Home |
Exponential and Logarithmic EquationsPart 1: Solving Exponential Equations We use the inverse properties to solve both exponential and logarithmic equations:
Question 5: Solve
Since the bases are the same we can set the exponents equal to each other.
Question 17: Solve
Here the bases are different so let's take logs of both sides.
Bring the exponents down in front of the logs.
Divide both sides by the constant
This is the exact solution. Question 43: Solve:
Multiply both sides by 2 to eliminate the fraction.
We can write this as Multiply both sides by
This is like a quadratic equation! Use the quadratic formula:
Take ln of both sides
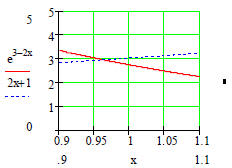
Question 49: Use MathCAD to solve graphically and
analytically:
Notice that there is a solution close to x =1. If we zoom in we can get a closer approximation: x = 0.96
MathCAD won't solve it if you use Symbolics-Variable-Solve. But if you use the Given-Find block. It will solve it numerically:
Part 2: Solving Logarithmic Equations
Question 30: Solve:
This is a quadratic equation Question 25: Solve:
Now raise both sides as exponents of 2
Solution is: Question 58: After a race, a runner's pulse rate R in beats per minute decreases according to the function
where t is measured in minutes. a) Find the runner's pulse at the end of the race and also 1 minute after the end of the race. b) How long, to the nearest minute, after the end of the race will the runner's pulse be at 80 beats per minute? a) b)
Solution is: Question 69: The velocity v of an object t seconds
after it has been dropped from a height above the surface of the earth is given
by the equation v = 32t feet per second, assuming no air resistance. If we
assume that air resistance is proportional to the square of the velocity, then
the velocity after t seconds is given by a) In how many seconds will the velocity be 50 feet per second? b) Determine the horizontal asymptote for the graph of this function. c) Write a sentence that describes the meaning of the horizontal asymptote in the context of this problem. a) We need to solve
Multiply both sides by the denominator .
b) Change the function to
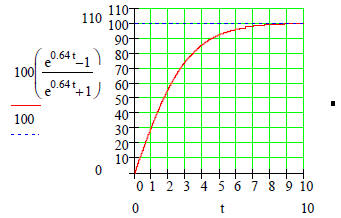
Now as t gets large without bound, the two little fractions disappear. So the horizontal asymptote is y = 100. See the graph below.
c) The maximum (terminal) velocity of the object is 100
feet per second |
||


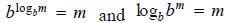
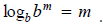
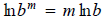
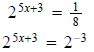
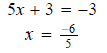
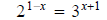
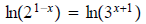
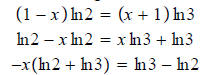
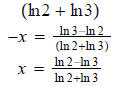
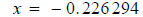
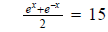
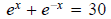
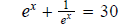
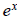 to eliminate the fraction.
to eliminate the fraction. 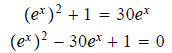
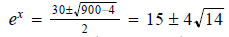
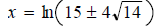
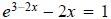
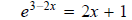
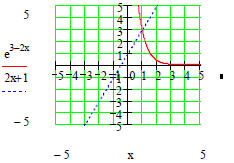
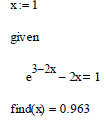
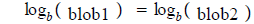
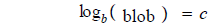
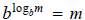 and take logs of both sides to
rewrite the equation with without logs.
and take logs of both sides to
rewrite the equation with without logs.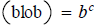
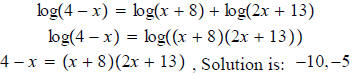
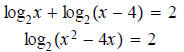
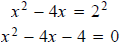
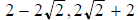
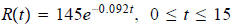
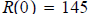 beats per minute at
the end of the race
beats per minute at
the end of the race 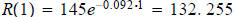 beats per minute
beats per minute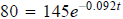 and solve for t.
and solve for t.