|
|
Solving Quadratic Equation
1. The equation is of the form a(x − h)^2 + k = 0
Corresponding parabola or quadratic function: y = a(x − h)^2 + k
Solutions are x-intercepts of this parabola
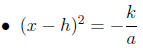
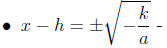 don’t forget ± sign don’t forget ± sign
• Solutions are 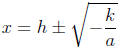
• Simplify and write as 2 separate numbers if − k/a is a
perfect square
2. The equation is not in the above form.
• If the equation is not in the form ax^2 + bx + c = 0,
then bring every term on one
side of “=”, foil (if necessary) and simplify to ax^2 + bx + c = 0
Corresponding parabola or quadratic function: y = ax^2 + bx + c
Solutions are x-intercepts of this parabola
• The solution is 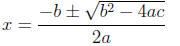
Simplify and write as 2 separate numbers if b^2 − 4ac is a
perfect square
You will get:
| Discriminant
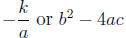 |
Type of solution (*
if p, q, r or a, b, c are integers) |
Graphically |
| positive perfect
square
not a perfect square |
2 real solutions 2
rational solution*
2 real solution with radicals
conjugate to each other |
2 x-intercepts
parabola crosses x-axis twice |
| zero |
1 rational solution* |
only 1 x-intercept
parabola just touches x axis |
| negative |
2 complex solutions
conjugate to each other |
no x-intercept
parabola does not intersect x axis |
Graphing Quadratic Function: Vertical Parabola
1. The function is in the form y = a(x − h)^2 + k
• Plot the points (h, k), (h + 1, k + a) and (h − 1, k + a)
• Draw the parabola through these points.
2. The function is in the form y = ax^2 + bx + c
• Plot the points:
y-intercept - (0, c), Point of symmetry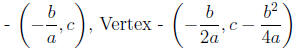 (or (or
plug in x = − b/2a into y = ax^2 + bx + c to get y-coordinate of vertex)
• Draw the parabola through these points.
• a > 0 - parabola opens up (smilie) with minimum at the
vertex
• a < 0 - parabola opens down (frownie) with maximum at the vertex
| |
y = a(x − h)^2 + k |
y = ax^2 + bx + c |
| vertex |
(h, k) |
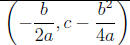 |
| axis |
x = h |
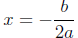 |
| symmetric points* |
(h + 1, k + a) and (h − 1, k + a) |
(0, c) and
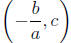 |
| y-intercept |
(0, ah^2 + k) |
(0, c) |
| x-intercept |
|
|
| none |
if k > 0 |
if b^2 < 4ac |
| one |
if k = 0 then (h, 0) |
if b^2 = 4ac then
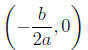 |
| two |
if k < 0 then 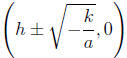 |
if b^2 > 4ac then
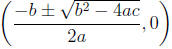 |
* These points are on opposite sides of the axis, at equal
distance from the axis and are at
the same height i.e. they have the same y-coordinate.
For horizontal parabola:
x = a(y − k)^2 + h - plot (h, k), (h + a, k + 1) and (h +
a, k − 1) and draw the parabola
x = ay^2 + by + c - plot (c, 0),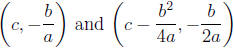 and draw the
parabola and draw the
parabola
a > 0 - parabola opens right, a < 0 - parabola opens left
|


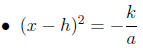
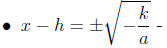 don’t forget ± sign
don’t forget ± sign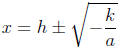
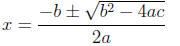
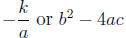
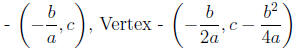 (or
(or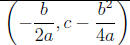
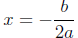
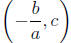
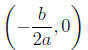
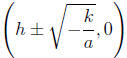
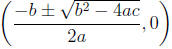
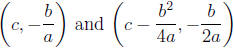 and draw the
parabola
and draw the
parabola