|
|
Linear Equations as Models
Big Idea: Linear equations in slope intercept form and
in standard form are used to write equations that represent real‐life
situations. Graphing will also lead to solving linear systems of equations and
inequalities.
Objectives of the Unit:
• Students correctly recognize how rate and value are
represented in an equation and a graph.
• Students accurately understand how the standard form of an equation for a line
is used to model situations.
• Students correctly change standard form to slope‐intercept form.
• Students describe slopes and write equations for horizontal and vertical
lines.
• Students can use two points to write an equation for a line.
• Students can use one point and the slope to write an equation for a line.
• Students can find the point where two lines intersect.
• Students graph linear inequalities on a coordinate plane.
• Students solve problems by writing and graphing systems of inequalities.
Student Outcomes:
M1.1.A Select and justify functions and equations to model
and solve problems.
M1.1.B Solve problems that can be represented by linear functions, equations and
inequalities.
M1.2.B Represent a function with a symbolic expression, as a graph, in a table,
and using words, and make connections
among these representations.
M1.3.B Describe how changes in the parameters of linear functions and functions
containing an absolute value of a linear
expression affect their graphs and the relationships they represent.
M1.3.D Write and graph an equation for a line given the slope and the
y‐intercept, the slope and a point on the line, or two points on the line, and
translate between forms of linear equations.
M1.3.E Write and solve systems of two linear equations and inequalities in two
variables.
M1.3.H Determine the equation of a line in the coordinate plane that is
described geometrically, including a line through two given points, a line
through a given point parallel to a given line, and a line through a given point
perpendicular to a given line.
M1.8.A Analyze a problem situation and represent it mathematically.
Student Learning Outcomes for Integrated
1, Unit 8
| |
|
Self Assessment |
| Outcome: “I can…” |
Example |
Starting |
Getting there |
Got it! |
| 1. …Write an equation using the
slope-intercept form, make a table and a graph from information. |
Emilee had $950 in her account on Jan. 1, she
added $75 each month. Model the situation with a table, graph and slope. |
|
|
|
| 2. …Show examples of linear growth
and linear decay. |
List the characteristics and slope, and sketch a
Linear Growth & Linear Decay |
|
|
|
3. …Write an equation using the
standard form of a linear equation. |
Each baseball practice the pitching staff must
throw for 20 minutes. Brian can throw 3 fastballs per minute and 2
changeups per minute.a. Write an equation
for this situation.
b. Rewrite the equation in slope‐intercept form. |
|
|
|
4. …Find the vertical and horizontal
intercepts of an equation. |
Find the vertical and horizontal intercepts of
the equation:
y = ‐2x + 2 |
|
|
|
| 5. …Write equations and find the
slope of vertical and horizontal lines. |
Write an equation for each line:
a. The points (9,3) and (‐1,3) are on the line…
b. The slope is undefined, and the point (‐1,4) is on the
line… |
|
|
|
6. …Write an equation from two
points, and write an equation from
other information. |
Two points on a line are (1,‐2) and (5,4). Write
an equation for the line. What is the slope of the line? What is the
vertical intercept of the line? The slope of
a line is -1/2 and one point on the line is (3,4). Write an equation for
this line. What is the vertical intercept of the line? |
|
|
|
| 7. …Graph systems of linear
equations. |
The service charge on a checking account at
Columbia Bank is $5 per month plus $.15 per Debit Card withdrawal. The
service charge at Frontier Bank is $.25 per Debit Card withdrawal.
a. Write and solve a system of equations to model this situation. |
|
|
|
8. …Graph a linear inequality on a
Coordinate Plane. |
Graph the inequality: y ≥ ‐x
Graph the inequality: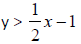
Graph the inequality: 5y – 3x ≥ 15 |
|
|
|
9. …Graph a system of inequalities to
answer a situation. |
Mr. Goldsberry has $600 to buy helmets and bats
for the team. He wants to buy at least 15 helmets and bats. Bats are $45
each and helmets are $35 each. Write and graph a system of inequalities
to model the situation. |
|
|
|
|