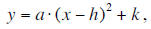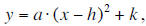Solving a Quadratic Equation
The most important points and skills for Section 5.5:
• Students are able to recognize formulas for quadratic functions in standard
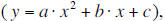 vertex vertex
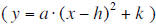 and factored and factored 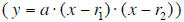 forms. forms.
• Given a graph of a quadratic function, f(x), that shows the locations of
two distinct x-intercepts and the
coordinates of one other point on the graph, students are able to find an
explicit formula for f(x) using
factored form.
• Given a graph of a quadratic function, f(x), that shows the coordinates of
the vertex and one other point
on the graph, students are able to find an explicit formula for f(x) using
vertex form.
• Given an explicit formula for a quadratic function, students are able to
determine the x- and y-coordinates
of the vertex and the axis of symmetry of the parabola by completing the square
and then
noting the values of h and k that are present in the vertex form,
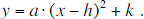
• Students should be able to determine the maximum/minimum of a quadratic
function by converting the
formula into vertex form and interpreting the meaning of the x- and
y-coordinates of the vertex in terms
of the “real-world” context described in word problems.
Comment:
Most students are already very familiar with quadratic functions, standard
form and factoring, however,
completing the square is quite difficult for many students. When you do examples
of completing the square,
avoid the temptation to cut corners and always describe your calculation methods
in full and put all steps in
your boardwork.
00-20 Use this time for a quiz or going over old homework. Section
5.3 #25 on page 217 and Section 5.4 #23
on page 224 are good problems to make sure you cover. 5.3 #25
emphasizes verbal interpretation of
functions. Problems like 5.4 #23 can be difficult for students who often
have trouble marking these type
of output values on a graph.
20-30 Begin the new material with a mini-review of what we’ve learned about
quadratic functions so far.
Remind them about the standard equation (y = ax^2+bx+c). This is also a good
time to remind them about
factored form (y = a(x-r1)(x-r2), where r1 and r2 are zeros) and what it means
to know the zeros of a
function. Introduce the third way of writing a quadratic function: vertex form
(y = a(x-h)^2+k). Make sure
to define the vertex and axis of symmetry as well as how these may be found in
an equation in vertex
form. (Note: at the end of the lesson plan, there is a handout that has been
used in previous terms
regarding vertex form and how it can be interpreted using function
transformations. Feel free to use it or
distribute to students if you would like.)
30-40 When you have established all of the terms,
have the students practice finding a formula for a quadratic
function when given the graph. Give the students two examples to try in their
groups. In the first
example, you could start with a graph that shows two x-intercepts and the
coordinates of one other point
(such as Section 5.5 #14 on page 231). For the second example, you could
start with a graph that shows
the coordinates of the vertex and the coordinates of one other point on the
graph (such as Section 5.5
#10 on page 231). Circulate as the groups work. Some questions that you
might find helpful to ask the
students are:
• Based on the information that you can see on the graph,
which way of writing a quadratic function
would be easiest to use here?
• How do the points you can see on the graph help you to
figure out the numbers that need to go into the
formula?
• What added information do we gain from the extra point
(i.e. not the zeros or vertex) on the graph?
• How can you know the sign of the leading coefficient
just by looking at the graph?
Generally, students understand how to use zeros and/or
vertex points in equations, but oftten have a
difficult time using the “extra” point to solve for the leading coefficient a.
40-55 Move into a graphical discussion of quadratic
equations by noting that all quadratic equations are
transformations of the function f(x) = x^2. Write the two equations f(x) = x^2
and g(x) = 3(x+7)^2-4 on the
board. Briefly, in their groups, ask students to discuss how the graph of g(x)
is related to the graph of
f(x) using terminology for transformations, and ask them to write g(x) in terms
of f(x). Next, write the
equation h(x) = 2x^2-8x+3 on the board. Note that because h(x) is quadratic, the
graph of f(x) should be
related to f(x) through various transformations. You can use this opportunity to
note that in standard
form, it is harder to determine how the graph of h(x) is related to f(x). Segue
into a mini-lecture about
completing the square and put h(x) into vertex form.
Note: The discussion of completing the square in the
Chapter 5 Tools section (page 239) of the textbook
gives a formula, but we don’t want to emphasize this. Rather, we want the
students to learn the
algorithmic approach that is used in Examples 1 and 2 (pages 239-240; also
Example 2 from pages 227-
228). If you really want to break down the technique into bite-sized pieces,
here is a procedure that you
could follow (for h(x) = 2x^2-8x+3).
Step 1: Factor out the leading coefficient
corresponding to x^2 out of every term in the function.
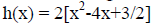
Step 2: Look at the number preceding the x-term.
Divide this number by 2 and then square that value.
number = -4 half the number = -2 squared = (-2)^2 = 4.
Step 3: Add and subract the value you computed in
Step 2 in between the x-term and constant term.
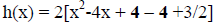
Step 4: Group together the first three terms to
have a perfect square.
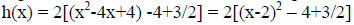
Step 5: Combine the constant terms left over
outside the perfect square.
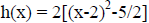
Step 6: Distribute the coefficient you factored out
in Step 1.
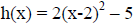
The most common mistakes are (i) not factoring a out of
everything in Step 1 and (ii) not distributing a
correctly in Step 6.
From the vertex form now found for h(x), students should
be able to easily comment about how the
graph of h(x) relates to the graph of f(x).
55-65 Have the students try a few examples of
completing the square. Pick a few exercises from Chapter 5
Tools Problems #13-#26 on page 241 for the students to try. A problem like
#23 can be a good one to
do since the students must factor out a negative number.
65-80 When you have confirmed that the students
have some level of proficiency with the procedure for
completing the square, you could demonstrate how this technique can be useful by
showing them how to
work through an optimization word problem. Have the students work in groups on a
problem like the
following:
The current price of a ticket at a local movie theater is
$8. At this price, the theater sells 1200 tickets
daily. The theater manager wonders if he will generate more revenue by
increasing the price of tickets.
For every dollar increase in ticket price, he will lose 100 ticket sales. What
ticket price will generate the
most revenue for the theater?
You can help the students tackle this problem by putting
the following subquestions to direct them.
i) Write a formula for the price, P, of a ticket that is raised d dollars.
Answer: P = 8 + d
ii) Write a formula for the number of tickets sold, T, based on a ticket price
increase of d dollars.
Answer: T = 1200 – 100d
iii) Write a formula for the revenue earned from ticket sales, R, depending on a
ticket price increase of d
dollars.
Answer: R = (price of ticket)(# tickets sold) = (P)(T) = (8+d)(1200-100d)
iv) You should have found that R is a quadratic function of d. Put R into
standard form.
Answer: R = -100d^2 + 400d + 9600
v) Find what value of d will maximize R by putting R into vertex form. (Why do
we know it’s a
maximum and not a minimum? Note that the leading coefficient is less than zero.)
Answer: R = -100(d-2)^2 + 10,000
vi) What is the price of the ticket, and how much revenue is generated?
Answer: A price increase of $2 will generate a maximum of $10,000
revenue. Therefore, the
price of the ticket is $8+$2 = $10.
If the students finish this quickly, you could help them
get started on their homework problems Section
5.5 #33 or #35 on page 232.
Wrap up the class by pointing out that the vertex form of
a quadratic function is very useful for optimization of
quadratic functions. Emphasize that they should understand Examples #5 and #6
on pages 230-231 from their
reading, and if they have questions regarding these problems, they should come
and see you in office hours.
Notes on Vertex Form and Transformations of Functions:
Why is the Vertex of a Quadratic Located at
(h, k)?
If you consider a quadratic function that is expressed in
vertex form, for example:
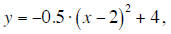
you might wonder just why it is that the vertex appears at
the point (2, 4). We will explain this by using
transformations to turn the basic quadratic y = x^2 into the new quadratic
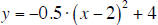 The The
transformations that we have to use to accomplish this will include a horizontal
shift of two units to the right
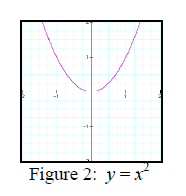
and a vertical shift of four units up. These transformations will move the
vertex of the basic quadratic (see
Figure 2) from (0, 0) to the point (2, 4).
To refresh your recollection of how transformations are
carried out algebraically and graphically, Table 1 shows
the effects of various transformations on the algebraic structure of the basic
quadratic y = x^2 and on the
appearance of its graph.
To convert the basic quadratic y = x^2 into the new
quadratic 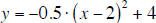 , you need to perform three , you need to perform three
transformation in the following order:
1. Horizontal translation (in this case by 2 units to the
right)
2. Vertical stretch/reflection (in this case there was a
vertical compression to half the usual height,
together with a reflection across the x axis).
3. Vertical translation (in this case by 4 units upwards).
So, the graph of 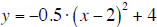 will
be a wide, upside down parabola that is displaced to the left and will
be a wide, upside down parabola that is displaced to the left and
above the origin. Confirming this graphically (see Figure 3), you can sketch
pictures to show the effect of each
transformation.
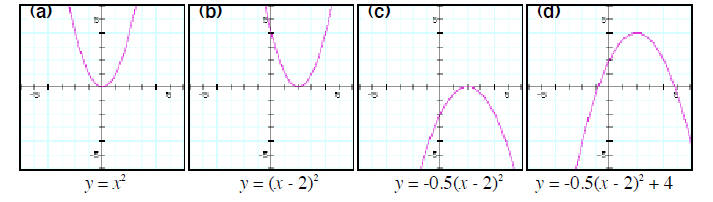
Figure 3: Note that the vertex of the basic quadratic y =
x^2 has been shifted from the point (0, 0) to the point (2, 4).
In a more general setting, in order to transform the basic
quadratic equation y = x^2 into the usual formula for
vertex form:
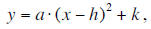
you would have to carry out the following transformations:
1. A horizontal shift of h units to the right.
2. A vertical stretch by a factor of a (which will also incorporate a reflection
across the x-axis if a is negative).
3. A vertical shift by k units upwards.
The horizontal shift will move the vertex of the quadratic
from (0, 0) to (h, 0) and the vertical shift will move
the vertex from (h, 0) to (h, k). This is why the vertex of the quadratic:
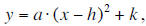
occurs at the point (h, k).
|


 vertex
vertex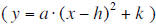 and factored
and factored 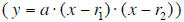 forms.
forms.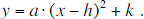
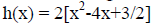
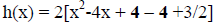
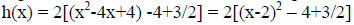
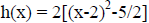
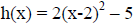
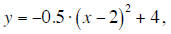
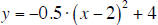 The
The
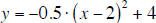 , you need to perform three
, you need to perform three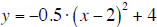 will
be a wide, upside down parabola that is displaced to the left and
will
be a wide, upside down parabola that is displaced to the left and