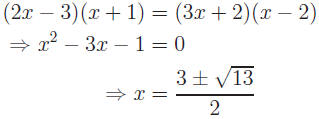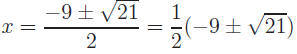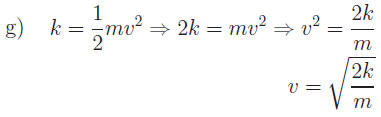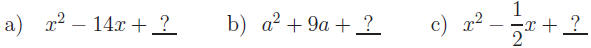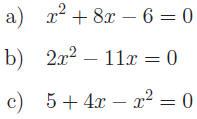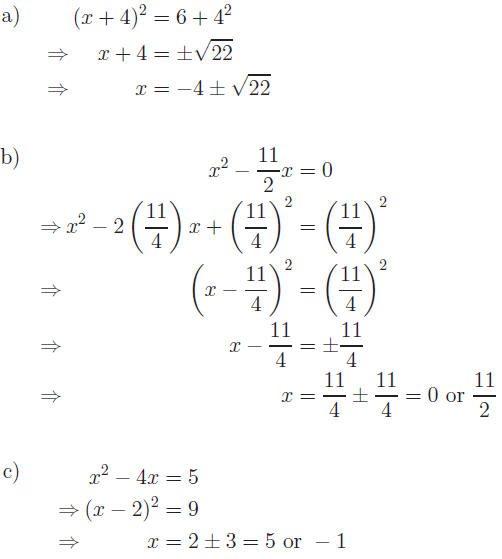Quadratic Equations
I. Finding Roots of a Quadratic Equation
A. Factoring
B. Quadratic Formula
C. "Taking Roots"
II. Guidelines for Finding Roots of a Quadratic
III. Completing the Square
A. Perfect Square Trinomials
B. Solving Quadratics by Completing the Square
Answers to Exercises
Introduction:
Any equation that can be expressed in the form ax2 + b x + c = 0, a ≠
0 is called
a quadratic equation.
Illustration:
2x2 + x − 6 = 0 quadratic in x
−16t2 + 80t = 0 quadratic in t:
The values that satisfy a quadratic (or any polynomial
equation) are called roots.
I. Finding Roots of a Quadratic Equation
There are 3 primary methods for finding roots to a quadratic. Here are
examples and comments on each.
A. Factoring
Consider the equation 2x2 + x − 6 = 0. When expressed as a
polynomial,
its roots are not easily apparent. Notice what happens if we rewrite this
expression in factored form:
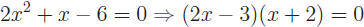
The roots now become clear:
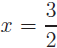 or x = −2. When solving a quadratic or x = −2. When solving a quadratic
equation, factored form has a distinct advantage over polynomial form. Any
value that turns a factor into 0 will automatically make the overall product
into 0 (and is therefore a root).
In "algebreeze" (that strange language used by math instructors), if a b = 0,
then a = 0 or b = 0.
Example: Solve x (x − 4) = 5.
Warning: You can only make use of factors when their product is 0.
If the problem read x (x−4) = 0, you would have roots of 0 and 4. No such
conclusions about roots can be drawn from x (x − 4) = 5.
Our only recourse is to remove parentheses and put into a b = 0 form.
Solution:
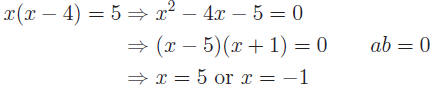
Example: Solve 9x2 = x.
Solution:
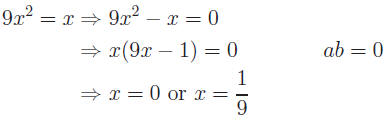
What if you attempted the same problem using the following
method?
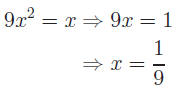 |
divide by x |
| |
Every quadratic equation has 2 roots. Dividing by x
removes the root x = 0.
However, dividing by a constant does not effect roots.
Example: Solve −16t2 + 80t = 0.
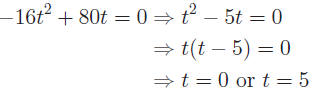 |
divide by (−16) |
| |
| |
Here's one last example of how factoring finds roots.
Example: x3 + 3x2 − 4x − 12 = 0.
Even though the example is not quadratic, any factorable polynomial can
be solved using the same principles.
Solution:
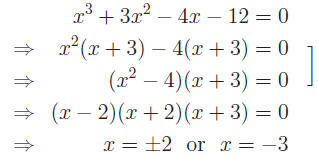 |
|
Grouping
Review Topic 4 |
| |
Exercise 1: Solve for x.
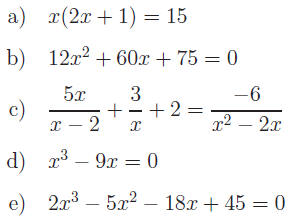 |
|
| Hint: Find LCD and clear fractions. |
| |
Answers
B. Quadratic Formula
Another method for finding roots to a quadratic equation is the quadratic
formula.
For ax2 + b x + c = 0, a ≠ 0,
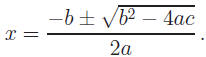
Example: Solve x2 − 6x − 4 = 0.
Solution: With a = 1, b = −6 and c = −4,
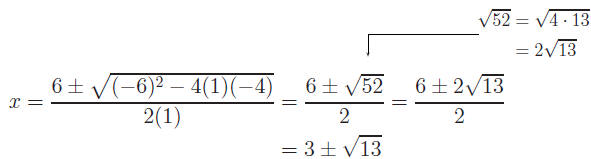
Any help you need with simplifying radicals can be found
in
Review Topic 6.
Comments: A quadratic has real roots when b2 − 4ac ≥0. The discussion
of non-real or complex roots (when b2 −4ac < 0) will be left for the
course.
C. "Taking Roots"
For quadratics with no middle term (when b = 0), the simplest approach is
to take square roots of both sides of the equation.
Example: Solve 3x2 − 4 = 0.
Solution:
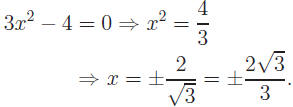 |
isolate x2 and take roots. |
| |
Common error: Don't forget the negative root.
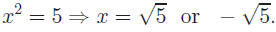
Example: Solve (x − 2)2 = 17.
You could expand the binomial, put into quadratic form and solve. Instead,
as in the previous example, square root both sides of the equation.
Solution:

It will help if you keep this example in mind when looking
at Section III of
this topic, completing the square.
Exercise 2: Find all real solutions.
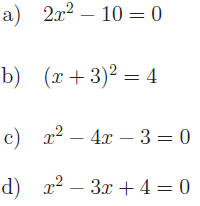
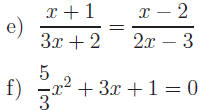
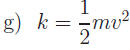 for v (Kinetic energy) for v (Kinetic energy)
Answers
II. Guidelines for Finding Roots of a Quadratic
You should now be able to solve quadratic equations using any of the three
methods shown: factoring, quadratic formula, or taking roots. Here is a
summary of what has been covered.
1) For ax2+c = 0, isolate x2 and square root both sides.
Don't forget the
negative root. Otherwise...
2) Put into the form ax2 + b x + c = 0. This may require removing paren-
theses or clearing fractions. Dividing out a constant is helpful but not
necessary.
3) Find roots by factoring or the *quadratic formula. If b2 − 4ac <
0, the
equation has no real roots.
4) Check solutions, especially if original equation is fractional.
*Don't overuse the quadratic formula. Factoring is an important skill to
maintain so use it at every opportunity.
III. Completing the Square
Section Ic) demonstrated how quadratics in the form (x ( )) 2 = k are
solved.
Illustration: (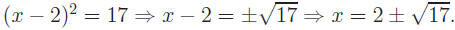
How is this related to completing the square? By expanding (x − 2)2
and
setting equal to 0, 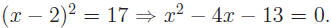 This would seem to This would seem to
indicate that any quadratic can be changed into (x ±( )) 2 = k form
(and
then solved). Such a process is called completing the square.
A. Perfect Square Trinomials
Completing the square requires a thorough understanding of how trinomials
of the form 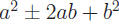 always factor into always factor into
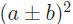 (Review Topic 4). (Review Topic 4).
Illustration:
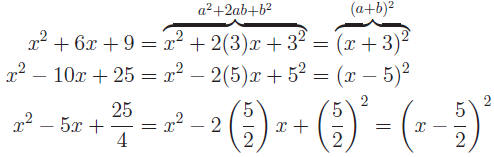
Trinomials such as these are referred to as Perfect Square
Trinomials (PST).
Exercise 3: Find the term needed to make a PST, then express in factored
form.
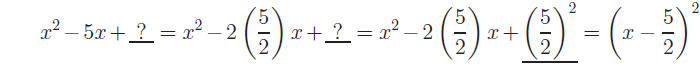
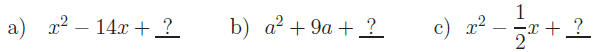 Answers Answers
B. Solving Quadratics by Completing the Square
Example: Solve x2 − 10x − 4 = 0.
Solution.
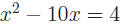 |
Move the constant so it
won't interfere with
completing the square |
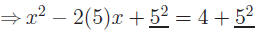 |
Comp. Square, maintain
equality by adding to both
sides |
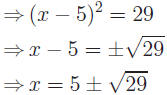 |
Factor and take roots |
Example: Solve 2x2 + 7x − 15 = 0
Solution.
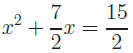 |
Divide out coef. of x2 |
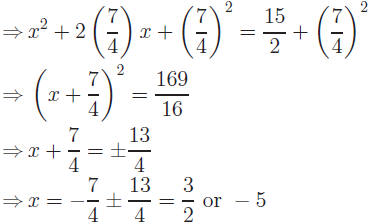 |
|
Why are these the roots of 2x2+ 7x − 15 = 0?
Check:
if 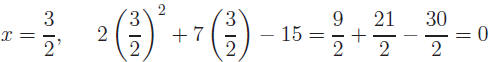
if x = −5, 2(−5)2 + 7(−5) − 15 = 50 − 35 − 15 = 0:
Final Comment: Completing the square may not be
your preferred
method for solving quadratics. However, the process is important to learn.
You will need to complete squares when working with equations of circles
and parabolas.
Exercise 4: Solve by completing the square.
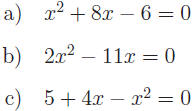
Answers
Beginning of Topic 108 Skills Assessment
Solve for x.
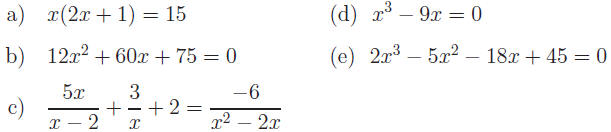
Hint: Find LCD and clear fractions.
Answers:
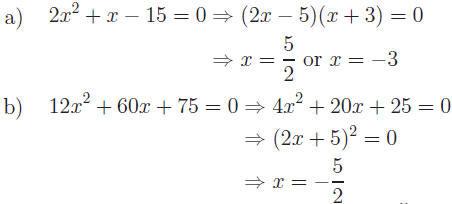
Since (2x + 5) is a repeated factor,
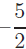 is a repeated or double root.
is a repeated or double root.
c) Multiply by x (x − 2) to clear fractions.
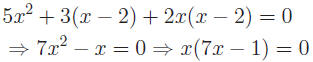
Thus x = 0 or 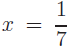 appear to be roots. Since division by 0 is
not
appear to be roots. Since division by 0 is
not
permissible, the only root is  . Always check roots when variables . Always check roots when variables
appear in any denominator.
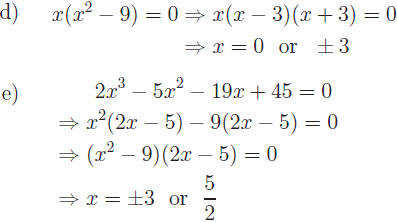
Find all real solutions.
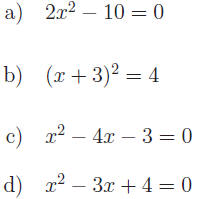
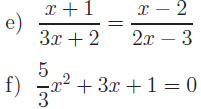
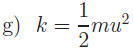 for v (Kinetic energy) for v (Kinetic energy)
Answers:
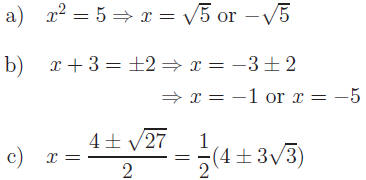
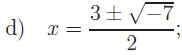 Since b2 − 4ac < 0, this
equation has no real roots. Since b2 − 4ac < 0, this
equation has no real roots.
e) Solving as a proportion,
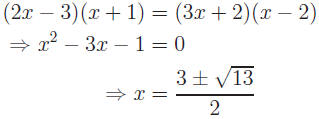
f) After clearing fractions, 5x2 + 9x + 3 = 0.
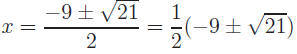
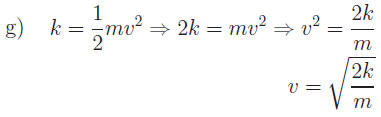 |
Since we solved for
velocity, disregard the
negative root. |
Return to Review Topic
Find the term needed to make a PST, then express in
factored form.
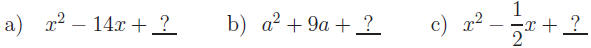
Answers:

Return to Review Topic
Solve by completing the square.
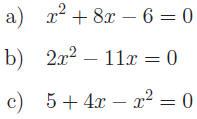
Answers:
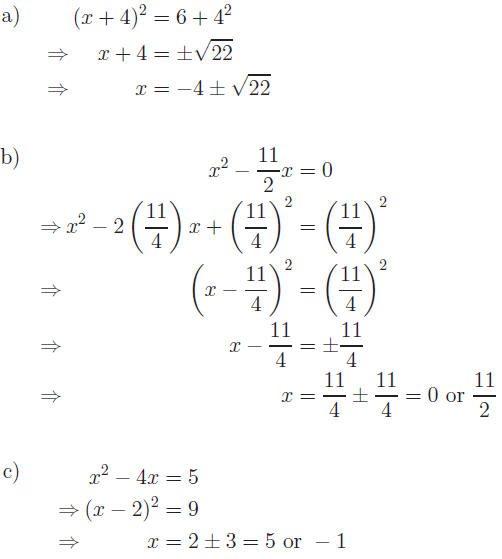
Return to Review Topic
|


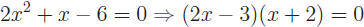
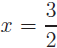 or x = −2. When solving a quadratic
or x = −2. When solving a quadratic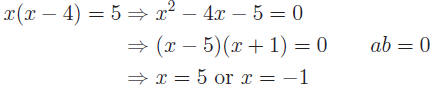
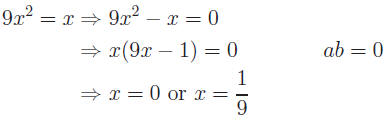
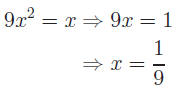
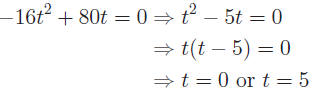
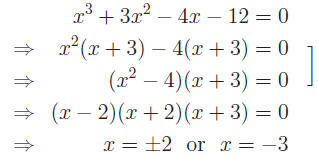
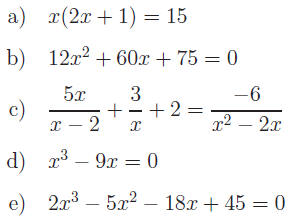
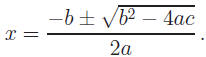
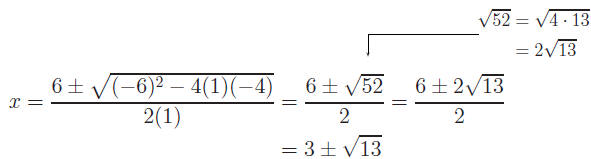
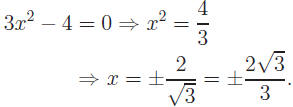
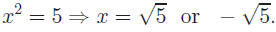

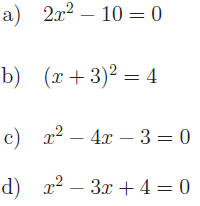
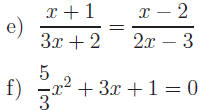
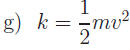 for v (Kinetic energy)
for v (Kinetic energy)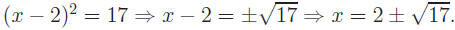
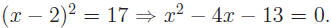 This would seem to
This would seem to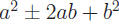 always factor into
always factor into
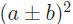 (Review Topic 4).
(Review Topic 4).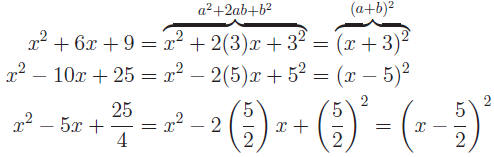
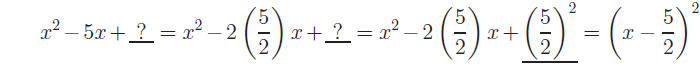
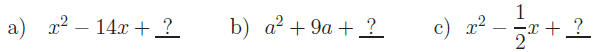 Answers
Answers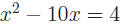
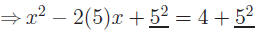
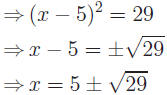
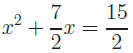
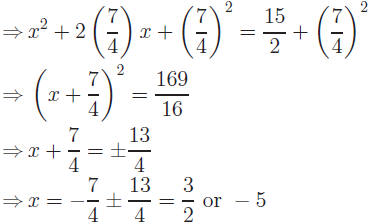
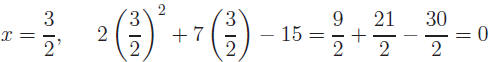
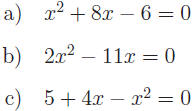
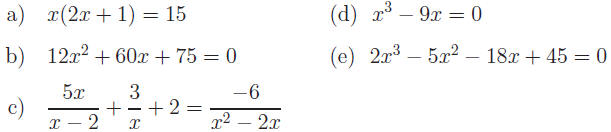
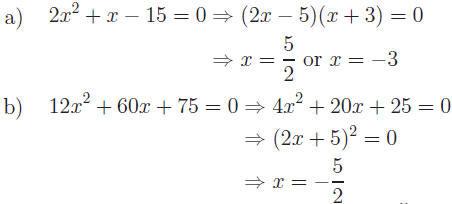
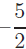 is a repeated or double root.
is a repeated or double root.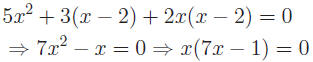
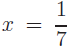 appear to be roots. Since division by 0 is
not
appear to be roots. Since division by 0 is
not  . Always check roots when variables
. Always check roots when variables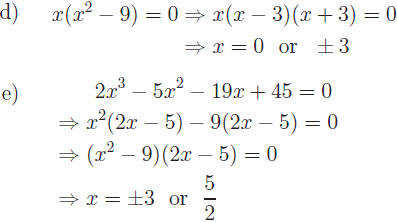
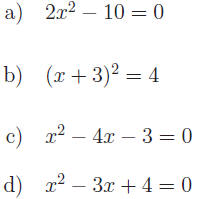
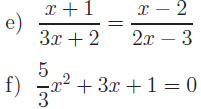
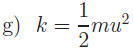 for v (Kinetic energy)
for v (Kinetic energy)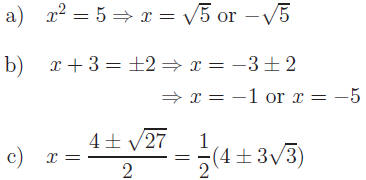
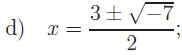 Since b2 − 4ac < 0, this
equation has no real roots.
Since b2 − 4ac < 0, this
equation has no real roots.