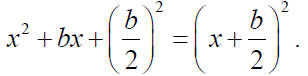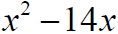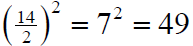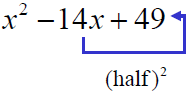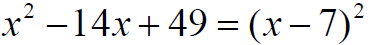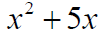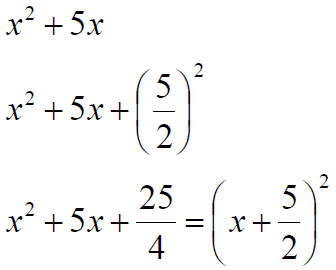|
Home |
Quadratic EquationsA quadratic equation in x is an equation that can be written in the standard from ax2 + bx +c = 0 where a, b, and c are real numbers with a ≠ 0. A quadratic equation in x is also called a second-degree polynomial equation in x The Zero-Product Principle If the product of two algebraic expressions is zero, then at least one of the factors is equal to zero. .If AB = 0, then A = 0 or B = 0. Solving a Quadratic Equation by Factoring 2.Factor. 3. Apply the zero-product principle, setting each factor equal to zero. 4. Solve the equations in step 3. 5. Check the solutions in the original equation. Ex 1 Solve by factoring:
Solution
Continued
Solution set is
Practice Exercises Solve:
Answers 1. Solution set 2.Solution set The Square Root Method
Ex 2 Solve by the square root method: Solution
Solution set: Completing the Square If x2 + bx is a binomial, then
by adding
Ex 3 What term should be added to the binomial
so that it becomes a perfect square trinomial? Add the constant
Factor the trinomial
Practice Exercise Determine the constant that should be added to the binomial so that it becomes a perfect square trinomial. Then factor the trinomial
Answer
|
||


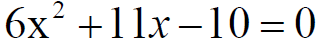
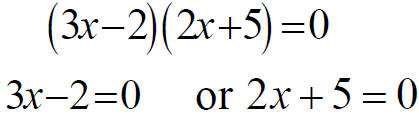
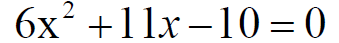
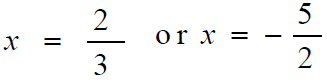
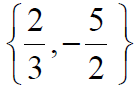
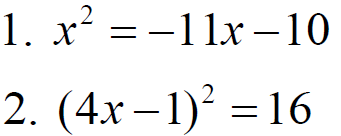
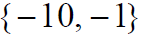
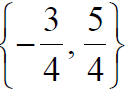
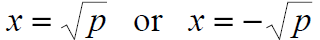
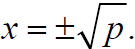
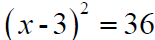

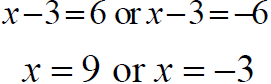
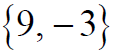
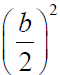 , which is the square of half the
coefficient of x, a perfect square trinomial will result..
, which is the square of half the
coefficient of x, a perfect square trinomial will result..