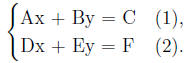Two Equations containing Two Variables
1 Geometric View of Two Linear Equations containing Two
Variables
Reminder of Linear Equation:
A linear equation containing two variables x, y is an equation of the form Ax +
By = C,
where A,B, and C are constants.
The graph of a linear equation containing the variables x, y is a LINE in xy-space.
Thus, a system of two linear equations containing the variables x, y is a PAIR
of LINEs
in xy-space.
A system of two linear equations containing two variables:
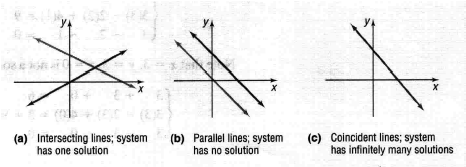
The above Figure shows 3 possible solutions of a system of
two linear equations containing
two variables:
• Exactly ONE solution (UNIQUE solution): the solution is
given by the point of intersection.
• NO solution.
• INFINITELY MANY solutions.
Note: It is NOT possible for a linear system to
have exactly two solutions.
A system of equations is said to be consistent if the system has AT LEAST ONE
solution.
If a system does not have a solution, the system is said to be inconsistent.
Two systems of linear equations are equivalent if the two systems have identical
solutions.
2 Solve System of Equations by Elimination
This method is ususally preferred over substitution if
substitution leads to fractions ot if the
system contains more than two variables.
The idea behind the method of elimination is to keep
replacing the original equations
in the system with EQUIVALENT equations until a system of equations with an
obvious
solution is reached.
Rules for Obtaining an Equivalent System of Equations
(Elementary Row
Operations)
• 1. Interchange any two equations of the system.
• 2. Multiply (or divide) each side of an equation by the same NONZERO constant.
• 3. Replace any equation in the system by the sum (or difference) of that
equation and
a NONZERO multiple of any other equation in the system.
The steps of the Method of Elimination:
Solve:
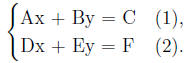
• 1. MULTIPLY each side of either equation (1) or (2) by
some nonzero number so that
the coefficients of x in the 2 equations are negatives of one another. According
to Rule
2, the result is the equivalent system to the original system.
• 2. REPLACE either equation (1) or (2) of the equivalent system by the SUM of
the
two equations. According to Rule 3, the result is the equivalent system to the
original
system with only one variable y. The variable x is eliminated.
Then, we can solve for y.
• 3. BACK-SUBSTITUTE by substituting the computed value of y back into either
equation (1) or (2).
Then, we can solve for x.
Notice: If you want, you can solve for x in Step 2,
and then solve for y in Step 3. In order to
do so, Step 1 becomes “MULTIPLY each side of either equation (1) or (2) by some
nonzero
number so that the coefficients of y in the 2 equations are negatives of one
another”.
Example 1:

Example 2:

Example 3:

|