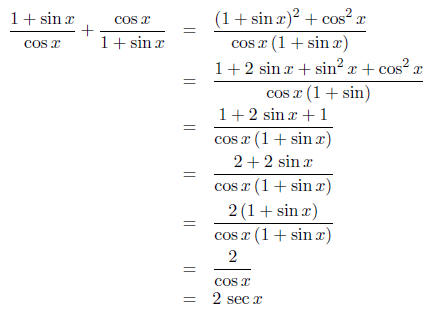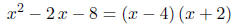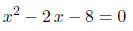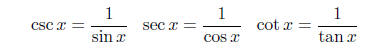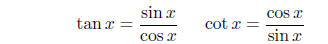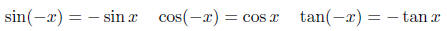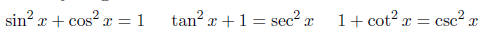|
Home |
Trigonometric Identities and
|
|
| Basic Trigonometric Identities For x any real number (in all restricted so that both sides of an equation are defined): Reciprocal Identities
Quotient Identities
Identities for Negatives
Pythagorean Identities
|
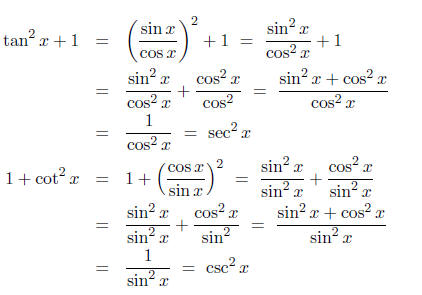
Establishing Other Identities
Identities are established in order to convert one form to an equivalent
form that may be more useful. To verify an identity means to prove that
both sides of an equation are equal for all replacements of the variables
for which both sides are defined. Such a proof might use basic identities,
factoring, combining and reducing fractions, and so on. The methods to
verify certain identities are not unique. To become proficient in the use
of identities, it is important that you work out many problems on
your own.
Example: Verify the identities
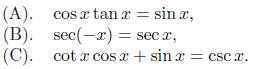
Solution. To verify an identity, we proceed by
starting with the more com-
plicated of the two sides, and transform that side into the other side in one
or more steps using basic identities, algebra, or other established identities.
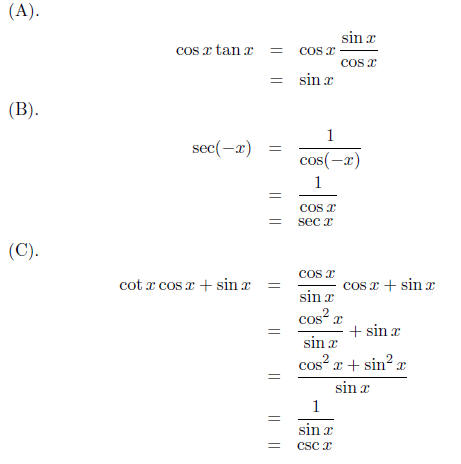
Suggested steps in verifying identities(Page 454 of the textbook)
(1) Start with the more complicated side of the
identity, and transform
it into the simpler side.
(2) Try algebraic operations such as multiplying, factoring, combining
fractions, and splitting fractions.
(3) If other steps fail, express each function in terms of sine and cosine
functions, and then perform appropriate algebraic operations.
(4) At each step, keep the other side of the identity in mind. This often
reveals what you should do in order to get there.
Review of the algebraic identities
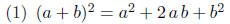
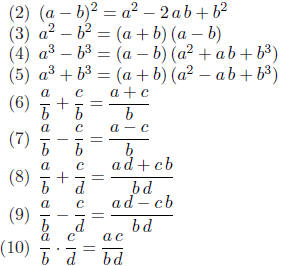
Example verify the identities
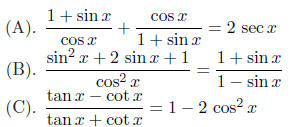
Solution. (A).