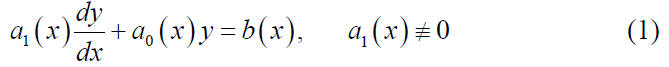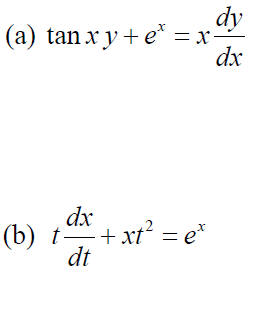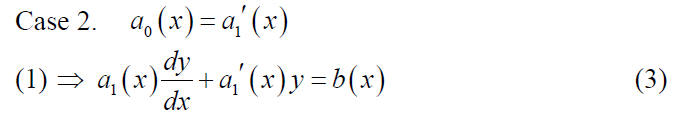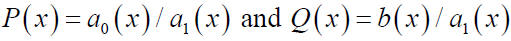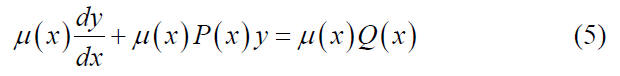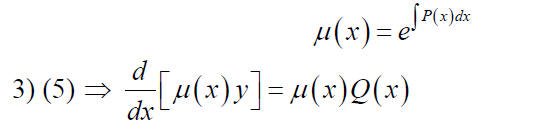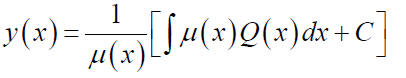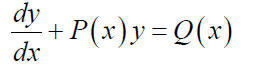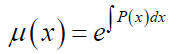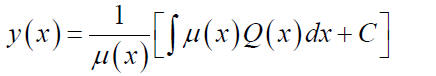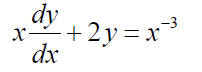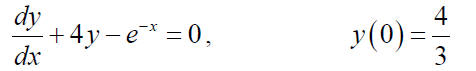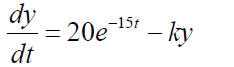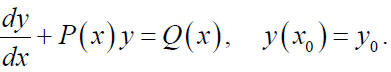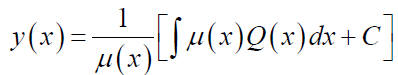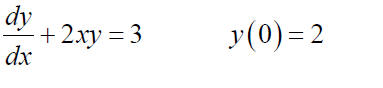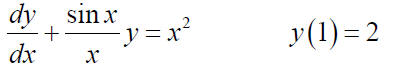Home
Linear Equations
Literal Equations
Simplifying Expressions & Solving Equations
Two Equations containing Two Variables
LinearEquations
Solving Linear Equations
Plane Curves Parametric Equation
Linear Equations and Matrices
LinearEquations
Test Description for EXPRESSIONS AND EQUATIONS
Trigonometric Identities and Conditional Equations
Solving Quadratic Equation
Solving Systems of Linear Equations by Graphing
SOLVING SYSTEMS OF EQUATIONS
Exponential and Logarithmic Equations
Quadratic Equations
Homework problems on homogeneous linear equations
Solving Quadratic Equations
LinearEquations
Functions, Equations, and Inequalities
Solving Multiple-Step Equations
Test Description for Quadratic Equations and Functions
Solving Exponential Equations
Linear Equations
Linear Equations and Inequalities
Literal Equations
Quadratic Equations
Linear Equations in Linear Algebra
SOLVING LINEAR AND QUADRATIC EQUATIONS
Investigating Liner Equations Using Graphing Calculator
represent slope in a linear equation
Equations
Linear Equations as Models
Solving Quadratic Equations by Factoring
Solving Equations with Rational Expressions
Solving Linear Equations
Solve Quadratic Equations by Completing the Square
LinearEquations
Solving a Quadratic Equation

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Linear Equations

L4 Linear Equations (Section 2.3)

Definition: A linear first order differential equation is an equation
that can be expressed in the form

Example:

Some Special Cases:

Discussion of the Method Involving an “Integrating Factor”:

1) Put the equation in the standard form:

where

2) Multiply both sides of the equation (4) by the integrating factor μ (x)

2) Determine μ (x) so that the left-hand side of the equation (5)
is the derivative of the product μ (x) y :

The general solution:

Method for Solving Linear Equations

(a) Write the equation in standard form

(b) Calculate the integrating factor μ (x) by the formula

where C is an arbitrary constant.

Example: Find the general solution to the equation

Example: Solve the initial value problem and find the value of y (−1).

Example: A rock contains two radioactive isotopes, RA₁ and RA₂ ,
that belong to the same radioactive series; that is, RA₁ decays into
RA₂ , which then decays into stable atoms. Assume that the rate at
which RA₁ decays into RA₂ is 20e^−15t kg/sec. Because the rate of
decay of RA₂ is proportional to the mass y (t ) of RA₂ present, the
rate of change in RA₂ is

[rate of change]= [rate of creation] – [rate of decay]

If k = 4 / sec and y (0) = 30 kg, find the mass y(t ) of RA₂ for t ≥ 0

Existence and Uniqueness of Solution for a Linear First-order
Differential Equation

Theorem 1. Suppose P(x) and Q(x) are continuous on the
interval (a,b) that contains the point x₀. Then for any choice of
initial value y₀ , there exists a unique solution y (x) on (a,b) to the
initial value problem

In fact, the solution is

for a suitable value of C.

(See problem 34 for the details on the proof)

Special Cases when the Definite Integral is Used

Example: Solve the initial value problem