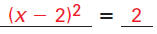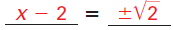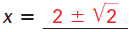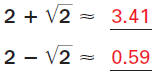Solve Quadratic Equations by Completing the Square
Goals • Solve quadratic equations by completing
the square.
Your Notes
VOCABULARY
Completing the square Adding a constant c to an
expression of the form x2 + bx to form a perfect
square trinomial
COMPLETING THE SQUARE
Words
To complete the square for the expression
x2 + bx, add the square of half the coefficient
of x.
Algebra
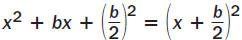
Example 1 Complete the square
Find the value of c that makes the expression
x2 - 5x + c a perfect square trinomial. Then write
the expression as the square of the binomial.
Solution
Step 1 Find the value of c.
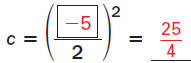
Find the square of half the
coefficient of x.
Step 2 Write the expression as a perfect
square trinomial.
Then write the expression as the square of a
binomial.
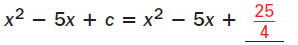 Substitute Substitute
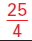 for c. for c.
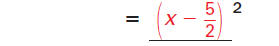 Square of a binomial Square of a binomial
● Guided Practice Find the value of c that makes the
expression a perfect square trinomial. Then write
the expression as the square of a binomial.
Example 2 Multiple Choice Practice
What quantity should be added to both sides of this
equation to complete the square?
x2 - 16x = 10
A -64
B -8
C 8
D 64
Solution
Find the square of half of the coefficient of x:
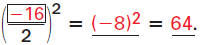
The correct answer is D . A B C D
Example 3 Solve a quadratic equation
Solve 4x2 - 16x + 8 = 0 by completing the square.
Solution
| |
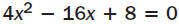 |
Write original
equation. |
| |
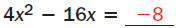 |
Subtract 8
from each side. |
Be sure that the
coefficient of x2
is 1 before you
complete the
square. |
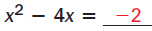 |
Divide each side
by 4 . |
| |
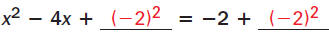 |
Add 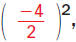 |
| |
|
or 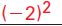 , to , to
each side. |
| |
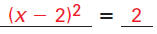 |
Write left side as
the square of a
binomial. |
| |
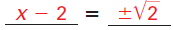 |
Take square roots
of each side. |
| |
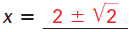 |
Add 2 to
each side. |
| |
The solutions are |
Check To check the solutions
of 4x2 16x + 8 = 0, graph
the related function.
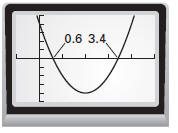

The x-intercepts are
approximately 0.6 and 3.4.
Compare these values with
the solutions:
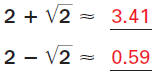
Homework
|


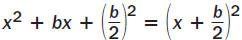
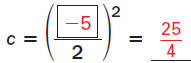
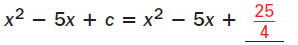 Substitute
Substitute
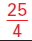 for c.
for c.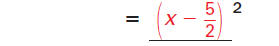 Square of a binomial
Square of a binomial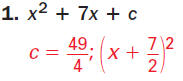
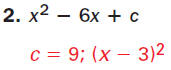
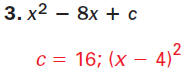
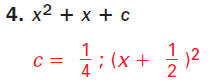
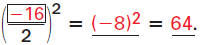
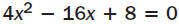
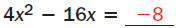
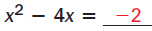
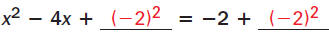
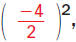
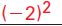 , to
, to