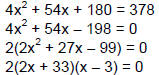|
|
Solving Quadratic Equations by Factoring
I. Solving Word Problems - Procedure
A. Read the problem.
B. Define a variable to represent the unknown.
C. Write an equation expressing the situation.
D. Solve the equation.
E. Answer the question with a complete sentence.
II. Solving Quadratic Equations by Factoring
A. Procedure
1. Write the equation in standard from.
2. Factor completely.
3. Set each factor that has a variable in it equal to 0.
4. Solve each equation.
5. Check your answer.
6. Note that the number of solutions will be the same as the degree of the
polynomial.
III. Quadratic Models
A. On these, we usually are given a formula. We have to determine where to
substitute
the numbers into the formula.
B. Examples - Solve each of the following.
1. A ball is thrown straight up from a rooftop 300 feet high. The formula:
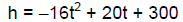
describes the ball's height above the ground, h, in feet,
t seconds after it was
thrown. The ball misses the rooftop on its way down and eventually strikes
the ground. The graph of the formula is shown, with tick marks omitted along
the horizontal axis (middle of right-hand column, page 451).
When will the ball's height be 304 feet? Identify the solution as a point on the
graph. (Page 451, #68)
Let h = The height of the ball , in feet Let t = The time of flight, in seconds
We want to know when the ball is at a height of 304 feet. So which variable
do we substitute 304 in for in the model?
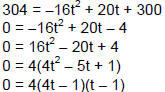 |
Subtract 304 from both sides to put in Standard
form. |
| Multiply both sides by -1 to make the Quadratic
Term positive. |
| Factor out the GCF of 4. |
| Factor the trinomial in the parentheses. |
| Use the Zero Product Property to solve for t. |
| 4t - 1 = 0 OR t - 1 = 0 |
| 4t = 1 OR t = 1 |
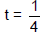 |
Note that we did not set 4 = 0 since there was no
variable. |
| Answer: |
The ball will be at a height of 304 feet after
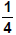 second and after 1 second. second and after 1 second. |
2. Now you try one: An explosion causes debris to rise
vertically with an initial
speed of 72 feet per second. The formula
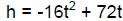
describes the height of the debris above the ground, h, in
feet, t seconds after
the explosion. When will the debris be 32 feet above the ground? (Page 451,
#71)
Answer: The debris will be 32 feet above the ground after
 second and after 4 second and after 4
seconds.
IV. Geometric Figures
A. The formulas for perimeter, area, and volume can be found in Section 2.6 of
your textbook.
B. Examples - Solve each of the following.
1. The length of a rectangular garden is 5 feet greater than the width. The area
of the
rectangle is 300 square feet. Find the length and the width. (Page 452, #82)
Let w = The width of the garden Let w + 5 = The length of the garden
We know that the formula for the area of a rectangle is A = LW. We know that the
area is 300 and we have expressions for the length and the width. So now we need
to write an equation expressing this situation.
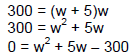 |
Distribute to clear parentheses on the right-hand
side.
Subtract 300 from both sides to write in Standard Form.
Factor the trinomial. Find the factors of 300 that when subtracted give
5. |
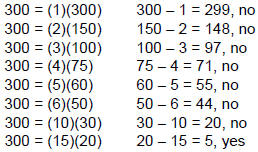 |
| 0 = (w + 20)( w - 15) |
Use the Zero Product Property to solve for the
variable. |
| w + 20 = 0 OR w - 15 = 0 |
| w = -20 OR w = 15 |
| OOPS! |
Answer the question. |
| Answer: |
The garden is to be 15 feet by 20 feet. |
2. A vacant rectangular lot is being turned into a
community vegetable garden measuring
15 meters by 12 meters. A path of uniform width is to surround the garden. If
the
area of the lot is 378 square meters, find the width of the path surrounding the
garden.
(Page 453, #86)
Let x = The width of the path
First, we have the following relationship:

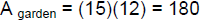 square meters square meters
To find 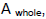 we need
to come up with expressions for the length and the width. But we need
to come up with expressions for the length and the width. But
we are starting with the garden and then we are adding the width of the path on
both
sides. What this means is:
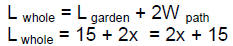
We go through a similar process for the width of the whole
thing.
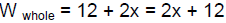
So now we can find the area of the whole thing.
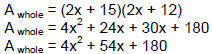 |
Distribute to clear parentheses on the right-hand
side. |
| Combine like terms to simplify the
right-hand side. |
Thus now we can write an expression for the area of the
path.
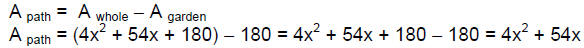
However, this is not what we needed for #86, but you will
use this idea for #87a (so
no, I'm not going senile in my old age!).
We have found that the 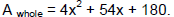 But we are given that But we are given that
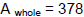 . .
So using substitution, we set these two expressions for A whole equal to each
other.
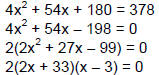 |
Subtract 378 from both sides to put in Standard
Form.
Factor out the GCF of 2.
Factor the trinomial in the parentheses.
Use the Zero Product Property to solve for the variable. |
| 2x + 33 = 0 OR x - 3 = 0 |
| 2x = -33 |
x = 3 |
| OOPS! |
Answer the question. |
| Answer |
The path is to be 3 meters wide. |
|


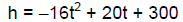
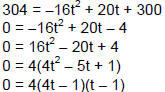
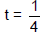
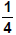 second and after 1 second.
second and after 1 second.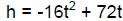
 second and after 4
second and after 4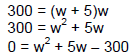
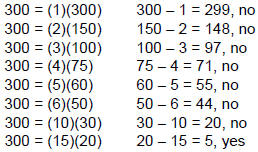

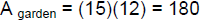 square meters
square meters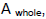 we need
to come up with expressions for the length and the width. But
we need
to come up with expressions for the length and the width. But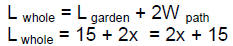
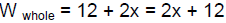
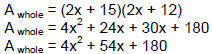
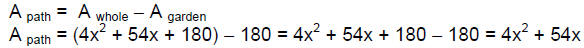
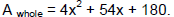 But we are given that
But we are given that
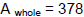 .
.