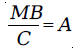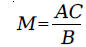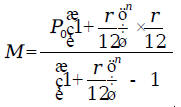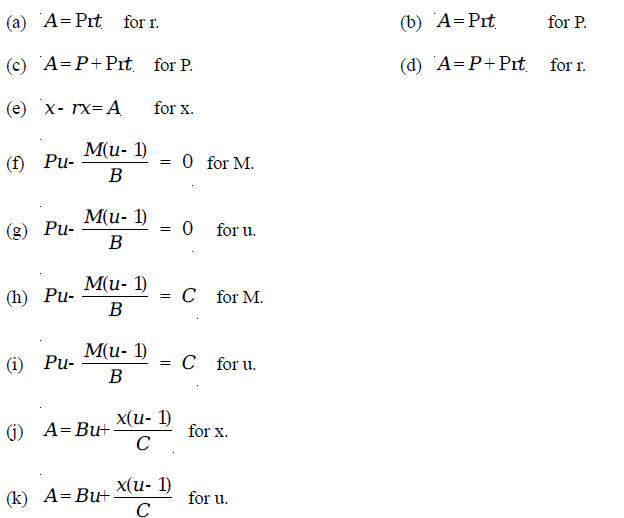|
Home |
Linear Equations3.1 Linear equationsWe encounter many situations in which we have to solve
linear equations (that is, Consider the problem: What is the number x which when multiplied by 8 gives 125? We know at once that the number x must be greater than 10
since 10 times 8 is 80 but less x(8) = 125 ___ or ___ Since 8 times x is to be 125, we reason that x must be the
number that is obtained by So, the number is ___ or ___ . The number ___ or ___ is
called the solution of To solve more complicated problems, we make use of the
following properties of (i) If equals are added to equals, the results are equal. Since subtraction of a number is defined to be the
addition of its negative, the statement, We can formally solve the simple equation given above as follows: Of course, we do not write in such great detail, but it is
important to know the principles Example 1: Find the solution of the equation Solution: We will write out the solution in great detail.
Once you get used to, you The idea is to bring the equation to the form ax = b by
making use of the or To get rid of ___ from the right-hand side, we add ___ to
both sides of or and so Example 2: Find the solution of the equation 5(3t+ 2) = 2(5t+ 7)+ 8 . Solution: Here the first problem is to simplify both sides of the equation:
Therefore, the solution of the equation is 2.4. Example 3: Find the solution of the equation
Solution: Here again the first step is to simplify the
left-hand side of the equation.
The solution is 3.55. Exercises 3.1 1. Find the solution of each of the following equations:
(You should check your
3.2 Literal equationsWe often have to solve an equation for one of the
variables in terms of the other Example 1: A man wants to buy a new car priced at
$18,000, financing it at 5.75% We could have substituted the values into the installment purchase formula
and obtained the equation
We can solve this equation as follows:
So, the monthly payment is $345.90. Or we can substitute the values in the monthly payment formula
and get
which is exactly the same as the value obtained above. Let us review how we obtained the monthly payment formula
from the installment We let
Then, we have
We have to solve this equation for M. Adding
Multiplying both sides of the equation by C and then
dividing both sides of the equation
Substituting back, we get the monthly payment formula:
Exercises 3.2 Solve each of the equations for the indicated variable:
|


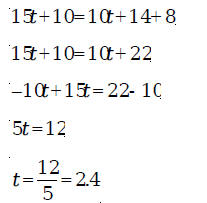
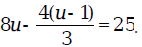
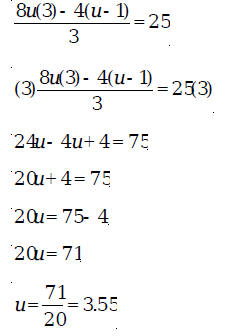
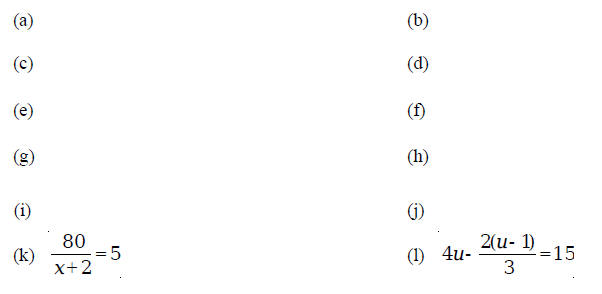
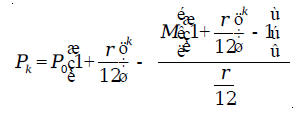
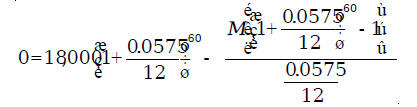
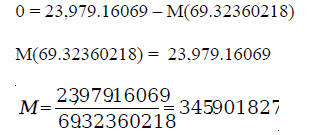
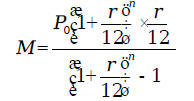
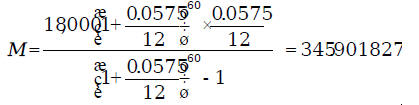
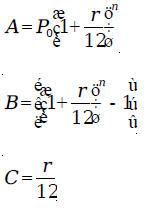
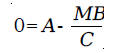
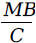 to both sides of the equation, we get
to both sides of the equation, we get